Insertion Sort
Insertion Sort is a simple and efficient algorithm for small datasets. It builds the sorted array one element at a time by repeatedly picking the next element and inserting it into the correct position among the previously sorted elements.
Insertion Sort is often compared to the way people sort playing cards in their hands, making it intuitive and easy to understand.
In this tutorial, we will go through the algorithm for Insertion Sort, with a well detailed example explained in steps, and time complexity.
Algorithm
Here are the steps of the Insertion Sort algorithm:
- Start with the second element (index 1) of the array as the current element.
- Compare the current element with the elements before it.
- If the current element is smaller than the compared element, shift the compared element to the right.
- Repeat step 3 until the correct position for the current element is found.
- Insert the current element at its correct position.
- Move to the next element and repeat steps 2-5 until the entire array is sorted.
Example
Let’s sort the array [5, 3, 8, 4, 2] using Insertion Sort and explain each step:
Initial Array:

Pass 1:
Current Element: 3
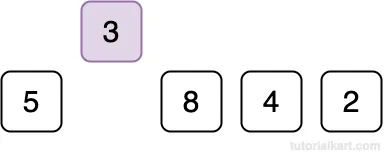
Compare 3 with 5.
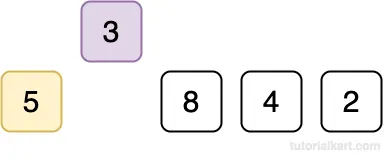
Since 3 < 5, shift 5 to the right.
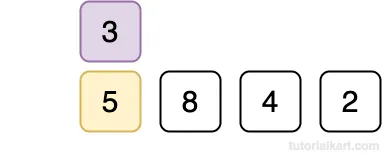
Insert 3 at index 0.

Array after pass 1.

Pass 2:
Current Element: 8
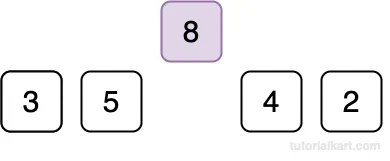
Compare 8 with 5.
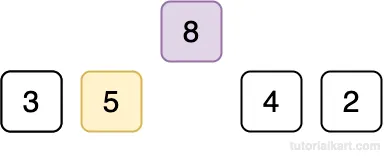
Since 8 > 5, no shifting is needed. 8 stays in its position.

Pass 3:
Current Element: 4
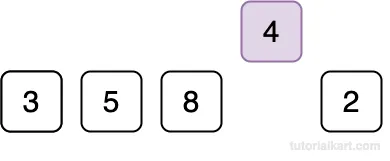
Compare 4 with 8.
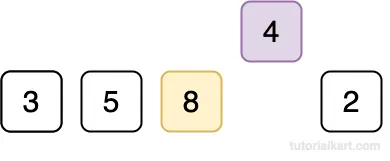
Since 4 < 8, shift 8 to the right.
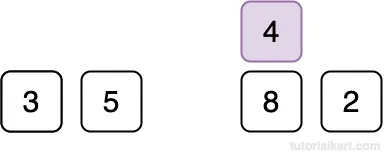
Compare 4 with 5.
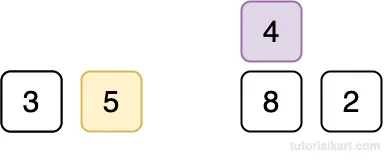
Since 4 < 5, shift 5 to the right.
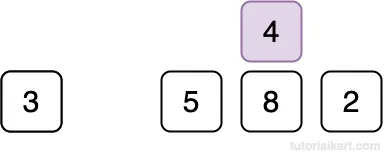
Compare 4 with 3.
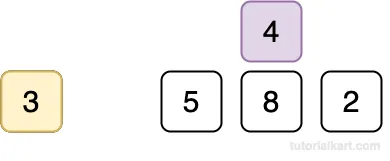
Since 4 > 3, the comparison is stopped, and 4 is inserted into the index 1.

Pass 4:
Current Element: 2
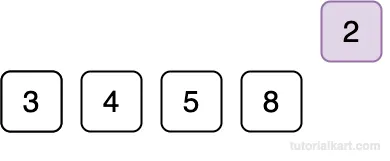
Compare 2 with 8.
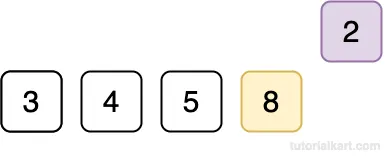
Since 2 < 8, shift 8 to the right.
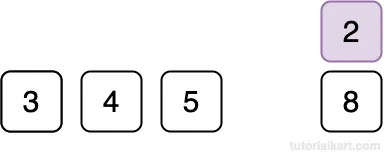
Compare 2 with 5.
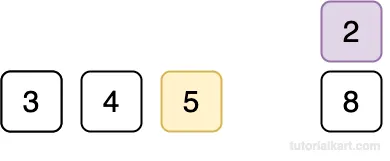
Since 2 < 5, shift 5 to the right.
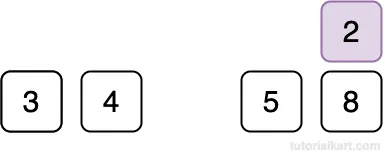
Compare 2 with 4.
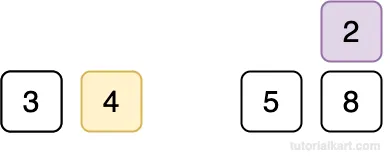
Since 2 < 4, shift 4 to the right.
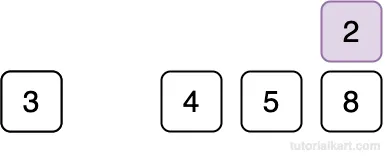
Compare 2 with 3.
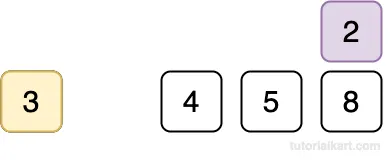
Since 2 < 3, shift 3 to the right.
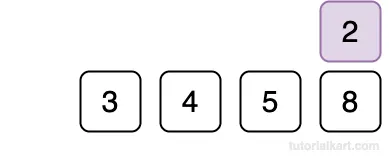
Insert 2 at index 0.

Final Sorted Array:

Complexity of Insertion Sort
1 Time Complexity:
The time complexity of Insertion sort for an array can vary based on the order of items in a given input array.
Worst-Case Complexity (\(O(n^2)\)):
This occurs when the array is sorted in reverse order, requiring the maximum number of comparisons and shifts.
Average-Case Complexity (\(O(n^2)\)):
On average, each element must be compared with half of the already sorted elements.
Best-Case Complexity (\(O(n)\)):
If the array is already sorted, each element only needs to be compared once.
2 Space Complexity:
Insertion Sort is an in-place algorithm, meaning it does not require additional space for another array. Its space complexity is \(O(1)\).
3 Stability:
Insertion Sort is a stable sorting algorithm. Equal elements maintain their relative order after sorting.
Insertion Sort Programs in Different Programming Languages
1 Go Program for Bubble Sort
Reference: Insertion Sort Program in Go
Program – insertion_sort.go
package main
import "fmt"
// Function to implement Insertion Sort
func insertionSort(arr []int) {
n := len(arr)
for i := 1; i < n; i++ {
key := arr[i]
j := i - 1
// Move elements of arr[0..i-1] that are greater than key
// to one position ahead of their current position
for j >= 0 && arr[j] > key {
arr[j+1] = arr[j]
j--
}
arr[j+1] = key
}
}
func main() {
// Input array
arr := []int{64, 34, 25, 12, 22, 11, 90}
// Display the original array
fmt.Println("Original array:", arr)
// Sort the array using Insertion Sort
insertionSort(arr)
// Display the sorted array
fmt.Println("Sorted array:", arr)
}Output
Conclusion
Insertion Sort is simple, efficient for small datasets, and adaptive for nearly sorted arrays. However, it is not suitable for large datasets due to its \(O(n^2)\) time complexity in the worst and average cases.
