Merge Sort
Merge Sort is a highly efficient, comparison-based sorting algorithm that uses the divide and conquer technique. It divides the array into smaller subarrays, sorts them, and then merges them back together to produce the sorted array. Merge Sort is particularly effective for large datasets due to its consistent time complexity of \(O(n \log n)\) in all cases.
In this tutorial, we will go through the Merge Sort Algorithm steps, a detailed example to understand the Merge Sort, and the Time and Space Complexities of the sorting algorithm.
Algorithm
Here are the steps of the Merge Sort algorithm:
- If the array has one or no elements, it is already sorted. Return the array. (Base Case)
- Divide the array into two halves. (Recursive Step)
- Recursively apply Merge Sort to the first half. Go to Step 1 for this half.
- Recursively apply Merge Sort to the second half. Go to Step 1 for this half.
- Merge the two sorted halves into one sorted array. (Merging Step)
- Return the merged array as the sorted result.
Example
Let’s sort the array [5, 3, 8, 4, 2] using Merge Sort and explain each step.
The following is the overview of how the divide and merge sort algorithm works for given array.
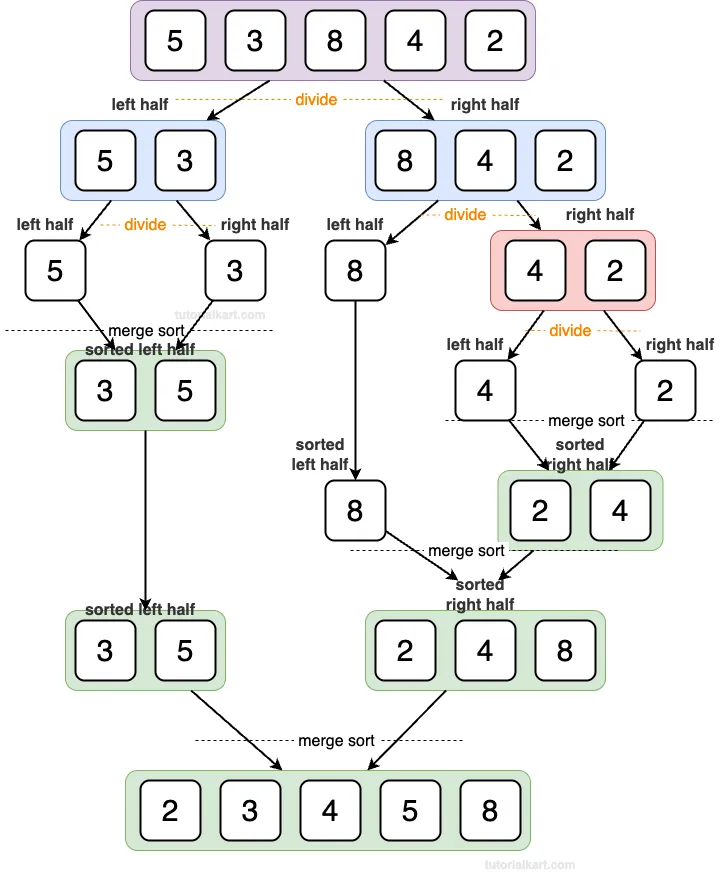
Initial Array:

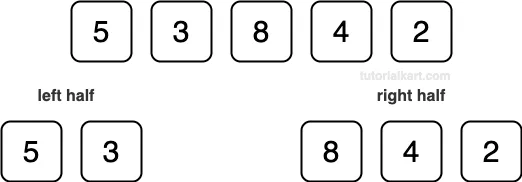
Step 1: Divide the Array
Divide the array into two halves:
Step 2: Recursively Sort Each Half
Sorting the Left Half [5, 3]:
- Divide [5, 3] into [5] and [3].
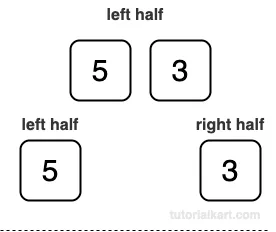
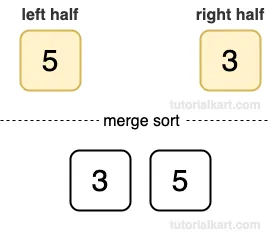
- Each subarray has one element, so it is already sorted.
- Merge [5] and [3]: Compare 5 and 3. The result is [3, 5].
Sorting the Right Half [8, 4, 2]:
- Divide [8, 4, 2] into [8] and [4, 2].
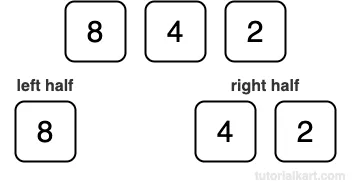
- [8] is already sorted. Sort [4, 2]:
- Divide [4, 2] into [4] and [2].
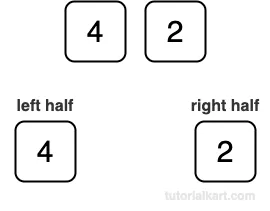
- Each subarray has one element, so it is already sorted.
- Merge [4] and [2]: Compare 4 and 2. The result is [2, 4].
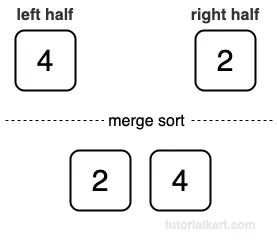
- Divide [4, 2] into [4] and [2].
- Merge [8] and [2, 4]: Compare 8 with 2 and 4. The result is [2, 4, 8].
Compare 8, 2. The smaller one is 2.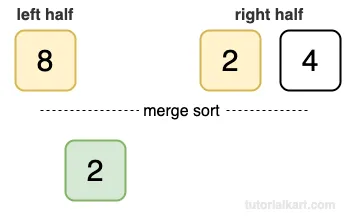
Compare 8, 4. The smaller one is 4.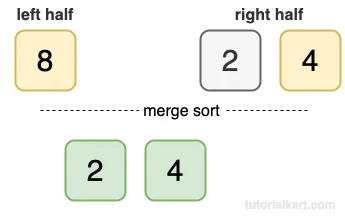
8 is the last one.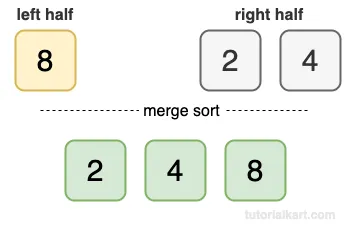
Step 3: Merge the Two Halves
Now merge the sorted halves [3, 5] and [2, 4, 8]:
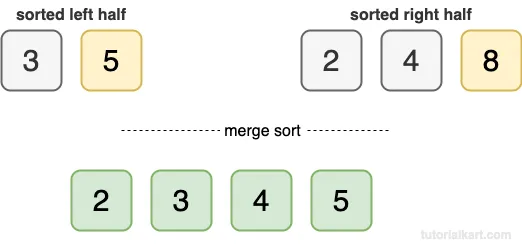
- Compare 3 and 2. Add 2 to the result.
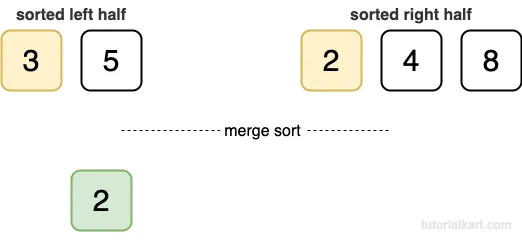
- Compare 3 and 4. Add 3 to the result.
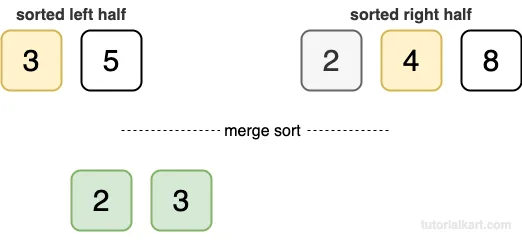
- Compare 5 and 4. Add 4 to the result.
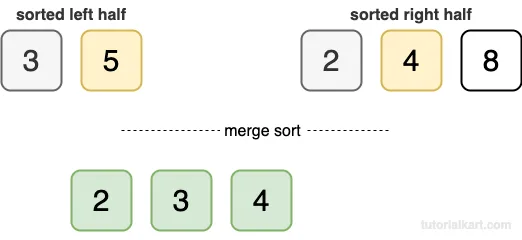
- Add the remaining elements 5 and 8 to the result.

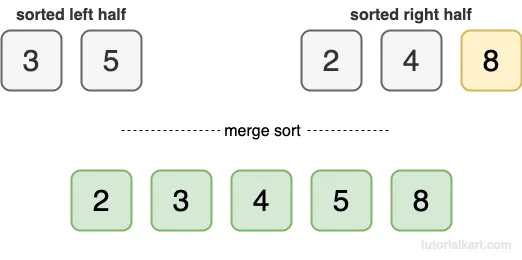
Final sorted array:

Complexity of Merge Sort
1 Time Complexity:
The time complexity of Merge Sort is (\(O(n \log n)\)) irrespective of the best or worst scenario.
Worst-Case Complexity (\(O(n \log n)\)):
The array is always divided into two halves, and merging takes linear time.
Average-Case Complexity (\(O(n \log n)\)):
Same as the worst case, since the division and merging steps are consistent.
Best-Case Complexity (\(O(n \log n)\)):
Even if the array is already sorted, it still undergoes division and merging.
2 Space Complexity:
Merge Sort requires additional memory for temporary arrays during the merging process, resulting in a space complexity of \(O(n)\).
3 Stability:
Merge Sort is a stable sorting algorithm, meaning that equal elements maintain their relative order in the sorted array.
Merge Sort Program in Different Programming Languages
Go Program for Merge Sort
Reference: Go Merge Sort
Program – merge_sort.go
package main
import "fmt"
// Function to merge two sorted slices
func merge(left, right []int) []int {
merged := []int{}
i, j := 0, 0
// Merge the two slices into a sorted slice
for i < len(left) && j < len(right) {
if left[i] <= right[j] {
merged = append(merged, left[i])
i++
} else {
merged = append(merged, right[j])
j++
}
}
// Append any remaining elements from the left slice
for i < len(left) {
merged = append(merged, left[i])
i++
}
// Append any remaining elements from the right slice
for j < len(right) {
merged = append(merged, right[j])
j++
}
return merged
}
// Recursive function to implement Merge Sort
func mergeSort(arr []int) []int {
if len(arr) <= 1 {
return arr
}
// Find the middle index
mid := len(arr) / 2
// Divide the array into left and right halves
left := mergeSort(arr[:mid])
right := mergeSort(arr[mid:])
// Merge the sorted halves
return merge(left, right)
}
func main() {
// Input array
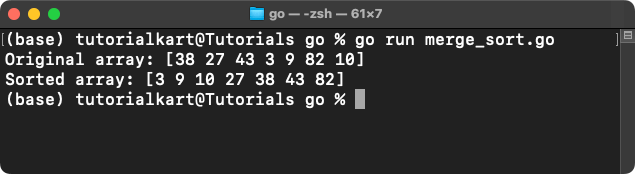
arr := []int{38, 27, 43, 3, 9, 82, 10}
// Display the original array
fmt.Println("Original array:", arr)
// Sort the array using Merge Sort
sortedArr := mergeSort(arr)
// Display the sorted array
fmt.Println("Sorted array:", sortedArr)
}Output
Conclusion
Merge Sort is an efficient and stable sorting algorithm suitable for large datasets. Although it requires additional memory, its predictable time complexity of \(O(n \log n)\) makes it a popular choice in many applications.
