Quick Sort Algorithm

Quick Sort

Quick Sort is a highly efficient, comparison-based sorting algorithm that uses the divide and conquer technique. It selects a pivot element, partitions the array around the pivot, and recursively applies the same process to the subarrays. Quick Sort is known for its average-case time complexity of \(O(n \log n)\) and is widely used for sorting large datasets.

In this tutorial, we will go through the Quick Sort Algorithm steps, a detailed example to understand the Quick Sort, and the Time and Space Complexities of this sorting algorithm.

Algorithm

Here are the steps of the Quick Sort algorithm:

If the array has one or no elements, it is already sorted. Return the array. (Base Case)
Choose a pivot element from the array. Common strategies include selecting the first, last, middle, or a random element.
Partition the array into two subarrays:
- Left subarray: Elements less than the pivot.
- Right subarray: Elements greater than or equal to the pivot.
Recursively apply Quick Sort to the left and right subarrays. Go to Step 1 for each subarray.
Combine the sorted subarrays and the pivot into one sorted array.

Example

The following is the overall picture of the quick sort for an array [5, 3, 8, 4, 2].

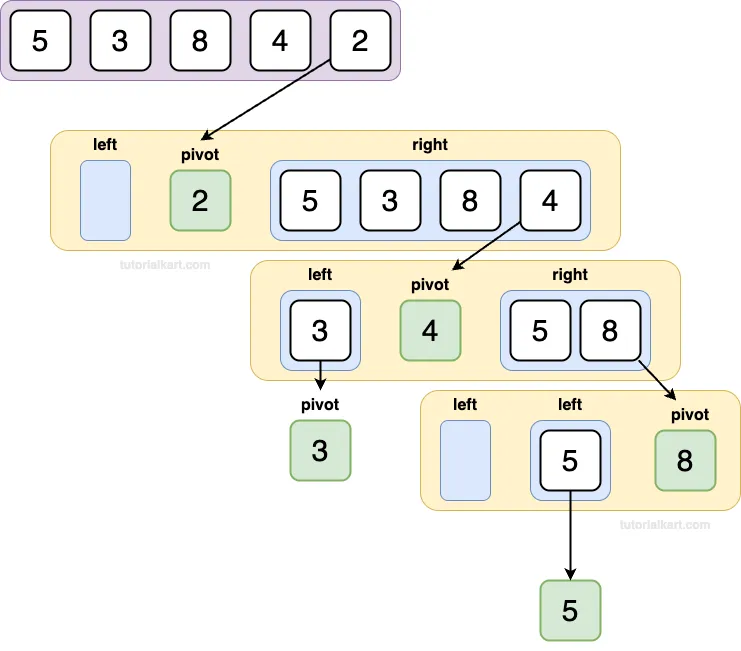
Let’s go through the step by step sorting of the array [5, 3, 8, 4, 2] using Quick Sort and explain each step:

Initial Array:

Step 1: Choose a Pivot

Choose the last element as the pivot: 2.

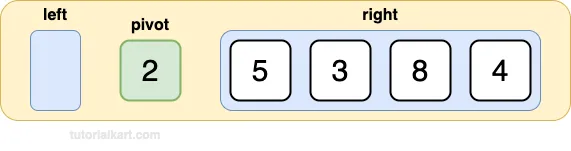
Step 2: Partition the Array

Partition the array into elements less than the pivot and elements greater than or equal to the pivot:

Left subarray: [] (no elements are less than 2)

Pivot: [2]

Right subarray: [5, 3, 8, 4]

Step 3: Recursively Sort Each Subarray

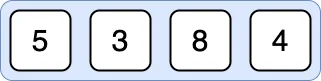
Sorting the Right Subarray [5, 3, 8, 4]:

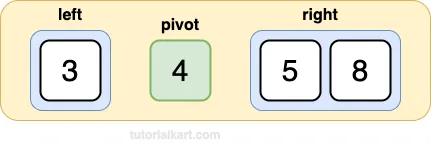
Choose the last element as the pivot: 4.

Partition the array:

Left subarray: [3] (elements less than 4)

Pivot: [4]

Right subarray: [5, 8] (elements greater than or equal to 4)

Sorting the Left Subarray [3]:

Array has one element, so it is already sorted.

Sorting the Right Subarray [5, 8]:

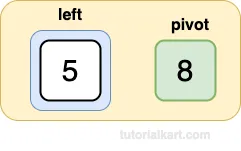
Choose the last element as the pivot: 8.

Partition the array:

Left subarray: [5]

Pivot: [8]

Right subarray: []

Both subarrays are already sorted.

Step 4: Combine the Sorted Subarrays

Combine the sorted subarrays and pivots:

[3] + [4] + [5, 8] = [3, 4, 5, 8]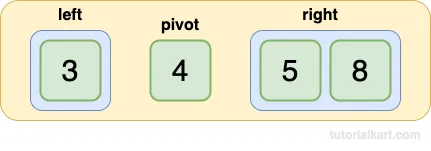

Step 5: Combine with the Pivot 2

Combine the left subarray, pivot, and sorted right subarray:

[] + [2] + [3, 4, 5, 8] = [2, 3, 4, 5, 8]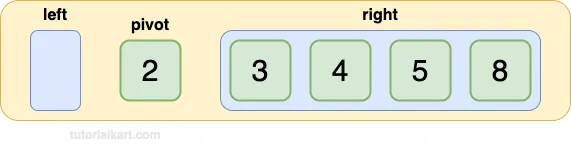

Final Sorted Array:

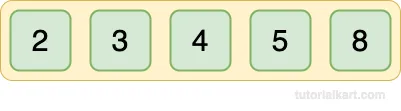
Complexity of Quick Sort

1. Time Complexity:

Worst-Case Complexity (\(O(n^2)\)):

This occurs when the pivot is the smallest or largest element, resulting in unbalanced partitions.

Average-Case Complexity (\(O(n \log n)\)):

On average, the array is evenly divided by the pivot, resulting in efficient sorting.

Best-Case Complexity (\(O(n \log n)\)):

The array is always divided into two equal halves by the pivot.

2. Space Complexity:

Quick Sort is an in-place algorithm when implemented iteratively, resulting in a space complexity of \(O(\log n)\) for recursive stack calls.

3. Stability:

Quick Sort is not a stable sorting algorithm. Equal elements may not maintain their relative order after sorting.

Quick Sort in Different Programming Languages

Go Program for Quick Sort

Reference: Go Quick Sort

Program – quick_sort.go

</>

Copy

package main

import "fmt"

// Function to partition the array
func partition(arr []int, low, high int) int {
    pivot := arr[high] // Choose the last element as pivot
    i := low - 1       // Index of smaller element

    for j := low; j < high; j++ {
        // If current element is smaller than or equal to the pivot
        if arr[j] <= pivot {
            i++
            // Swap arr[i] and arr[j]
            arr[i], arr[j] = arr[j], arr[i]
        }
    }
    // Swap arr[i+1] and the pivot element
    arr[i+1], arr[high] = arr[high], arr[i+1]
    return i + 1
}

// Function to implement Quick Sort
func quickSort(arr []int, low, high int) {
    if low < high {
        // Partition the array
        pi := partition(arr, low, high)

        // Recursively sort the sublists
        quickSort(arr, low, pi-1)
        quickSort(arr, pi+1, high)
    }
}

func main() {
    // Input array
    arr := []int{10, 7, 8, 9, 1, 5}

    // Display the original array
    fmt.Println("Original array:", arr)

    // Sort the array using Quick Sort
    quickSort(arr, 0, len(arr)-1)

    // Display the sorted array
    fmt.Println("Sorted array:", arr)
}

Output

Conclusion

Quick Sort is a fast and efficient sorting algorithm suitable for large datasets. While it is not stable, its average-case performance and in-place nature make it a popular choice in many applications.

TutorialKart