What is Space Complexity of an Algorithm?
Space complexity is a measure of the amount of memory an algorithm uses relative to the size of the input. It accounts for both the memory required by the variables in the program and the additional memory needed for the algorithm to execute.
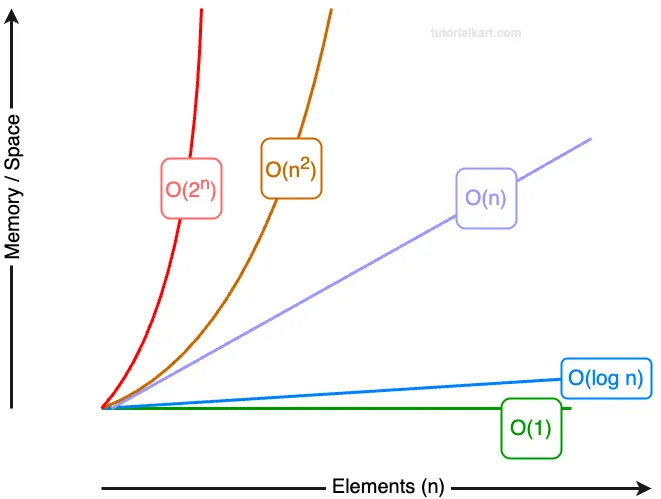
In simple terms, space complexity helps us understand how efficiently an algorithm uses memory resources.
Why is Space Complexity Important?
Space complexity is crucial for the following reasons:
- Ensures that algorithms run efficiently on devices with limited memory.
- Helps optimize memory usage in resource-constrained environments.
- Allows developers to choose between algorithms based on memory efficiency.
Components of Space Complexity
The space complexity of an algorithm consists of two main components:
Fixed Part: Memory required to store constants, variables, and program instructions. This does not depend on the size of the input.
Variable Part: Memory required to store the input, temporary variables, and data structures like arrays, stacks, and queues. This depends on the size of the input.
Types of Space Complexity
Space complexity can be categorised based on the memory usage of an algorithm:
1 Constant Space Complexity (\(O(1)\))
An algorithm with constant space complexity uses a fixed amount of memory regardless of the input size. For example, swapping two numbers requires \(O(1)\) space.
Example:
void swap(int a, int b) {
int temp = a;
a = b;
b = temp;
}
2 Linear Space Complexity (\(O(n)\))
An algorithm with linear space complexity uses memory that grows linearly with the input size. For example, storing an array of size \(n\) requires \(O(n)\) space.
Example:
int[] createArray(int n) {
return new int[n];
}
3 Logarithmic Space Complexity (\(O(\log n)\))
Algorithms with logarithmic space complexity use memory proportional to the logarithm of the input size. Recursive binary search is a common example.
Example:
int binarySearch(int[] arr, int target, int low, int high) {
if (low > high) return -1;
int mid = (low + high) / 2;
if (arr[mid] == target) return mid;
if (arr[mid] < target) return binarySearch(arr, target, mid + 1, high);
return binarySearch(arr, target, low, mid - 1);
}
4 Quadratic Space Complexity (\(O(n^2)\))
Algorithms with quadratic space complexity use memory proportional to the square of the input size. This often occurs in algorithms that involve creating a 2D matrix.
Example:
int[][] createMatrix(int n) {
return new int[n][n];
}
5 Exponential Space Complexity (\(O(2^n)\))
Algorithms with exponential space complexity use memory that grows exponentially with the input size. Recursive algorithms for problems like subsets or permutations often fall into this category.
Example:
void generateSubsets(String s, String current, int index) {
if (index == s.length()) {
print(current);
return;
}
generateSubsets(s, current, index + 1); // Exclude current character
generateSubsets(s, current + s.charAt(index), index + 1); // Include current character
}
Summary of Space Complexities

| Complexity | Notation | Example |
|---|---|---|
| Constant | O(1) | Swapping two numbers |
| Linear | O(n) | Storing an array |
| Logarithmic | O(log n) | Recursive binary search |
| Quadratic | O(n^2) | Creating a 2D matrix |
| Exponential | O(2^n) | Generating subsets |
Conclusion
Understanding space complexity is essential for designing algorithms that are memory-efficient and suitable for devices with limited resources. By analyzing both time and space complexity, developers can create optimal solutions for a wide range of problems.
