Time Complexity of an Algorithm

What is Time Complexity?

Time complexity is a measure of the computational time that an algorithm takes to run as a function of the size of the input. It helps us evaluate the efficiency of an algorithm and compare different algorithms to solve the same problem.

In simple terms, time complexity describes how the runtime of an algorithm grows with the size of the input.

---

Why is Time Complexity Important?

Time complexity is important because it allows us to:

1. Predict the performance of an algorithm on larger inputs.
2. Choose the most efficient algorithm for a specific problem.
3. Optimise programs and systems to reduce runtime.

---

Types of Time Complexity

Time complexity is categorised into the following types based on how the runtime of the algorithm scales with input size.

The following is an approximate graph showing different types of time complexities in Big-O notation. X-axis is the elements size. Y-axis the number of operations required by the algorithm.

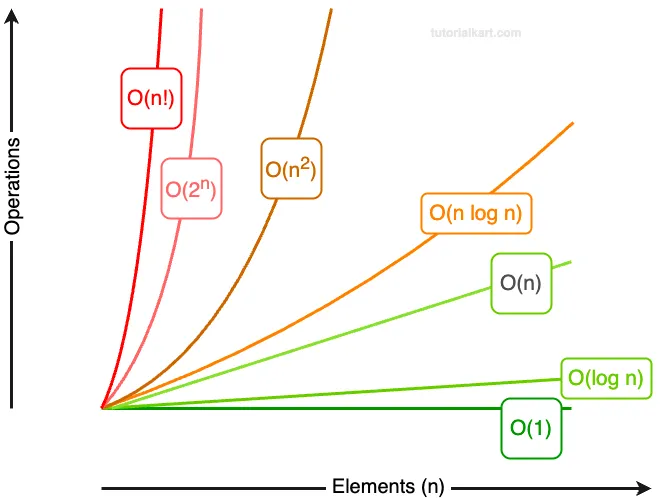
1. Constant Time Complexity ( \(O(1)\))

Constant Time Complexity is denoted as \(O(1)\) in Big-O notation.

An algorithm with constant time complexity runs in the same amount of time regardless of the input size. For example, accessing an element in an array by index is \(O(1)\).

Example:

int element = arr[5];

2. Linear Time Complexity (\(O(n)\))

Linear Time Complexity is denoted as \(O(n)\) in Big-O notation.

In linear time complexity, the runtime increases linearly with the size of the input. For example, traversing an array of size \(n\) takes \(O(n)\) time.

Example:

for (int i = 0; i < n; i++) {
    sum += arr[i];
}

3. Quadratic Time Complexity (\(O(n^2)\))

Quadratic Time Complexity is denoted as \(O(n^2)\) in Big-O notation.

An algorithm with quadratic time complexity scales with the square of the input size. Nested loops are a common example.

Example:

for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
        sum += arr[i] * arr[j];
    }
}

4. Logarithmic Time Complexity (\(O(\log n)\))

Logarithmic Time Complexity is denoted as \(O(\log n)\) in Big-O notation.

In logarithmic time complexity, the runtime grows logarithmically with the input size. Binary search is a typical example.

Example:

while (low <= high) {
    int mid = (low + high) / 2;
    if (arr[mid] == target) {
        return mid;
    } else if (arr[mid] < target) {
        low = mid + 1;
    } else {
        high = mid - 1;
    }
}

5. Exponential Time Complexity (\(O(2^n)\))

Exponential Time Complexity is denoted as \(O(2^n)\) in Big-O notation.

In exponential time complexity, the runtime doubles with each additional input size. Recursive algorithms for problems like the Traveling Salesman or subsets often have exponential complexity.

Example:

int fibonacci(int n) {
    if (n <= 1) return n;
    return fibonacci(n - 1) + fibonacci(n - 2);
}

6. Factorial Time Complexity (\(O(n!)\))

Factorial Time Complexity is denoted as \(O(n!)\) in Big-O notation.

Algorithms with factorial time complexity grow at an extremely fast rate. This complexity often arises in problems involving permutations.

Example:

void permute(int[] arr, int l, int r) {
    if (l == r) {
        print(arr);
    } else {
        for (int i = l; i <= r; i++) {
            swap(arr[l], arr[i]);
            permute(arr, l + 1, r);
            swap(arr[l], arr[i]); // backtrack
        }
    }
}

---

Summary of Time Complexities

Complexity	Notation	Example
Constant	O(1)	Accessing an array element
Linear	O(n)	Traversing an array
Quadratic	O(n^2)	Nested loops
Logarithmic	O(log n)	Binary search
Exponential	O(2^n)	Recursive algorithms
Factorial	O(n!)	Permutations

---

Conclusion

Understanding time complexity helps you analyse the performance of algorithms and make informed decisions about which algorithm to use for a given problem. While constant and linear complexities are efficient, quadratic, exponential, and factorial complexities can become infeasible for large inputs.