Deterministic Finite Automata (DFA)
A Deterministic Finite Automaton (DFA) is a type of finite automaton where every state has exactly one transition for each symbol in the input alphabet. This makes its behavior predictable and straightforward to understand. DFAs are widely used to model and analyze systems where determinism is required, such as lexical analyzers in compilers.
Key Properties of a DFA
DFAs have the following defining characteristics:
- Deterministic Transitions: For every state and every input symbol, there is exactly one transition to a next state.
- Finite States: A DFA has a finite number of states that define its possible configurations.
- Single Start State: The DFA begins processing from a specific initial state.
- Acceptance Condition: A DFA accepts an input string if, after processing all input symbols, it ends in one of its accept states.
Formal Definition
A DFA is formally defined as a 5-tuple (Q, Σ, δ, q₀, F), where:
- Q: A finite set of states.
- Σ: A finite input alphabet.
- δ: A transition function δ: Q × Σ → Q that maps a state and an input symbol to a single next state.
- q₀: The start state, where the DFA begins processing.
- F: A set of accept states, F ⊆ Q.
Examples for DFA
Example 1: DFA for Strings Example: DFA for Strings Containing ‘101’
Let’s create a DFA to recognize binary strings containing the substring ‘101’.
We need to construct a Deterministic Finite Automaton (DFA) to recognize strings over the alphabet Σ = {0, 1} that contain the substring ‘101’. A string is considered accepted if it contains this specific pattern anywhere in the input. For example:
- Accepted Strings:
'101','1101','0101','1010','10101' - Rejected Strings:
'1','0','100','110','111'
The DFA must correctly handle:
- Start state: Where the computation begins.
- Transitions: Moves between states based on the input character.
- Accept state: Where the DFA ends if the substring ‘101’ is found in the input.
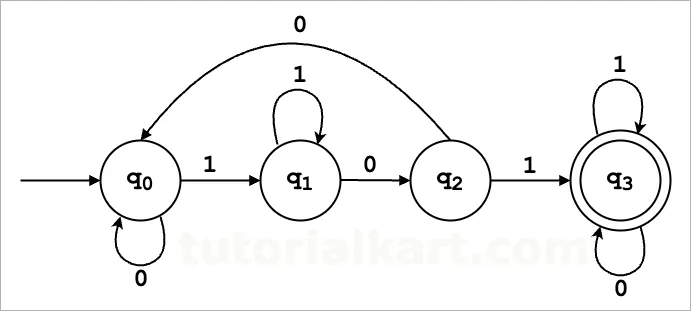
Components of the DFA
States, Q: {q₀, q₁, q₂, q₃}
- q₀: Initial state. Represents the scenario where no part of the substring ‘101’ has been identified yet.
- q₁: Represents that the input has ended with ‘1’.
- q₂: Represents that the input has ended with ’10’.
- q₃: Accept state. Represents that the substring ‘101’ has been detected.
Alphabets which are Input, Σ: {0, 1}
- The set of characters the DFA can read: Σ = {0, 1}.
Start State (q₀):
- The state where the DFA begins processing.
Accept State F: {q₃}
- q₃: The state where the DFA ends if the input string contains
'101'.
Transition Rules (δ):
These rules define how the DFA moves between states based on the input:
δ(q₀, '1') = q₁
δ(q₀, '0') = q₀
δ(q₁, '0') = q₂
δ(q₁, '1') = q₁
δ(q₂, '1') = q₃
δ(q₂, '0') = q₀
δ(q₃, '0') = q₃
δ(q₃, '1') = q₃δ(q₀, '1') = q₁: Transition from q₀ to q₁ on seeing ‘1’.δ(q₀, '0') = q₀: Stay in q₀ on seeing ‘0’ (no part of ‘101’ detected).δ(q₁, '0') = q₂: Transition from q₁ to q₂ on seeing ‘0’.δ(q₁, '1') = q₁: Stay in q₁ on seeing ‘1’.δ(q₂, '1') = q₃: Transition from q₂ to q₃ on seeing ‘1’ (completes ‘101’).δ(q₂, '0') = q₀: Transition from q₂ to q₀ on seeing ‘0’ (reset; no ‘101’).δ(q₃, '0') = q₃: Stay in q₃ on seeing ‘0’.δ(q₃, '1') = q₃: Stay in q₃ on seeing ‘1’.
State Diagram
Example 2: DFA for Even Length Inputs
Let’s create a DFA to recognise strings over the alphabet Σ = {a, b} that have an even length.
We need to construct a Deterministic Finite Automaton (DFA) to recognise strings over the alphabet Σ = {a, b} that have an even number of characters. A string is considered accepted if it contains an even number of symbols, regardless of the order. For example:
- Accepted Strings:
''(empty string),'ab','aa','abab','aabb' - Rejected Strings:
'a','b','aaa','aab','abb'
The DFA must correctly handle:
- Start state: Where the computation begins.
- Transitions: Moves between states based on the input character.
- Accept state: Where the DFA ends if the string is valid.
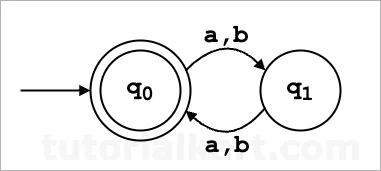
Components of the DFA
States, Q: {q₀, q₁}
- q₀: Initial state. Represents strings with an even length.
- q₁: Intermediate state. Represents strings with an odd length.
Alphabets which are Input, Σ: {a, b}
- The set of characters the DFA can read: Σ = {a, b}.
Start State (q₀):
- The state where the DFA begins processing.
Accept State F: {q₀}
- q₀: The state where the DFA ends if the string has an even number of characters.
Transition Rules (δ):
These rules define how the DFA moves between states based on the input:
δ(q₀, 'a') = q₁
δ(q₀, 'b') = q₁
δ(q₁, 'a') = q₀
δ(q₁, 'b') = q₀δ(q₀, 'a') = q₁: Transition from q₀ to q₁ on seeing ‘a’.δ(q₀, 'b') = q₁: Transition from q₀ to q₁ on seeing ‘b’.δ(q₁, 'a') = q₀: Transition from q₁ to q₀ on seeing ‘a’.δ(q₁, 'b') = q₀: Transition from q₁ to q₀ on seeing ‘b’.
State Diagram
Example 3: DFA for Alternate ‘a’ and ‘b’
Let’s create a DFA to recognise strings over the alphabet Σ = {a, b} where ‘a’ and ‘b’ strictly alternate.
We need to construct a Deterministic Finite Automaton (DFA) to recognise strings where each ‘a’ is followed by ‘b’ and vice versa. For example:
- Accepted Strings:
''(empty string),'ab','ba','abab','baba' - Rejected Strings:
'a','b','aa','bb','abaa'
The DFA must correctly handle:
- Start state: Where the computation begins.
- Transitions: Moves between states based on the input character.
- Accept state: Where the DFA ends if the string is valid.
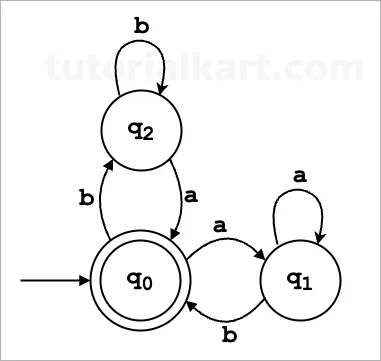
Components of the DFA
States, Q: {q₀, q₁, q₂}
- q₀: Initial state. Represents an empty string or one that follows the alternating pattern.
- q₁: Represents that the string ends with ‘a’ and is expecting ‘b’.
- q₂: Represents that the string ends with ‘b’ and is expecting ‘a’.
Alphabets which are Input, Σ: {a, b}
- The set of characters the DFA can read: Σ = {a, b}.
Start State (q₀):
- The state where the DFA begins processing.
Accept State F: {q₀}
- q₀: The state where the DFA ends if the alternating pattern is preserved.
Transition Rules (δ):
These rules define how the DFA moves between states based on the input:
δ(q₀, 'a') = q₁
δ(q₀, 'b') = q₂
δ(q₁, 'a') = q₁
δ(q₁, 'b') = q₀
δ(q₂, 'a') = q₀
δ(q₂, 'b') = q₂δ(q₀, 'a') = q₁: Transition from q₀ to q₁ on seeing ‘a’.δ(q₀, 'b') = q₂: Transition from q₀ to q₂ on seeing ‘b’.δ(q₁, 'a') = q₁: Stay in q₁ on seeing ‘a’ (violation).δ(q₁, 'b') = q₀: Transition from q₁ to q₀ on seeing ‘b’ (valid alternation).δ(q₂, 'a') = q₀: Transition from q₂ to q₀ on seeing ‘a’ (valid alternation).δ(q₂, 'b') = q₂: Stay in q₂ on seeing ‘b’ (violation).
State Diagram
Applications of DFA
DFAs are used in various real-world scenarios, such as:
- Lexical Analysis: Recognizing tokens in programming languages.
- Pattern Matching: Searching for specific patterns in text.
- Network Protocols: Modeling state transitions in communication protocols.
