Epsilon-NFA

Epsilon-NFA

An Epsilon-NFA (ε-NFA) is a type of nondeterministic finite automaton (NFA) that allows transitions without consuming any input symbols. These transitions are called epsilon transitions (or ε-transitions). This added flexibility makes ε-NFAs easier to construct for certain patterns, while still being computationally equivalent to both NFAs and DFAs.

---

Key Features of Epsilon-NFA

Here are the unique features of ε-NFAs:

1. ε-Transitions: The automaton can move from one state to another without reading an input symbol.
2. Nondeterminism: For a given state and input, the automaton may transition to multiple states, similar to an NFA.
3. Acceptance: An ε-NFA accepts a string if there exists at least one path, including ε-transitions, that ends in an accept state after processing the input.

---

Formal Definition

An ε-NFA is formally defined as a 5-tuple (Q, Σ, δ, q₀, F), where:

• Q: A finite set of states.
• Σ: A finite input alphabet.
• δ: A transition function, δ: Q × (Σ ∪ {ε}) → 2^Q, which maps a state and an input symbol (or ε) to a set of next states.
• q₀: The start state.
• F: A set of accept states, F ⊆ Q.

---

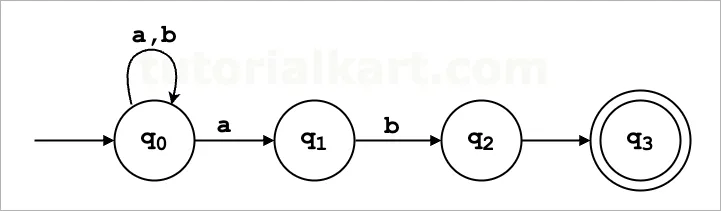
Example: ε-NFA for Strings Ending with ‘ab’

Consider an ε-NFA that recognizes strings over Σ = {a, b} that end with the substring ‘ab’. The ε-NFA can be defined as follows:

• States (Q): {q₀, q₁, q₂, q₃}
• Alphabet (Σ): {a, b}
• Start State: q₀
• Accept State: q₃
• Transition function: δ
  </>

  Copy

  δ(q₀, 'a') = {q₀, q₁}
  δ(q₀, 'b') = {q₀}
  δ(q₁, 'b') = {q₂}
  δ(q₂, ε) = {q₃}

Diagram: State diagram showing ε-transitions between q₂ and q₃, with other transitions as defined above.

---

Conversion of ε-NFA to NFA

To use an ε-NFA in practical applications, it is often converted into an equivalent NFA by eliminating ε-transitions. This is done using the following steps:

1. Calculate the ε-closure for each state (the set of states reachable from a given state using ε-transitions).
2. Update the transition function to account for ε-closures, ensuring that all ε-transitions are replaced with direct transitions between states.
3. Retain the original start state and determine new accept states based on the ε-closure of each accept state in the ε-NFA.

---

Key Takeaways

• ε-NFAs allow transitions without consuming input symbols, making them flexible and easier to design.
• They are equivalent to NFAs and DFAs, meaning every ε-NFA can be converted into an NFA or DFA.
• Understanding ε-NFAs is essential for mastering the theory of computation and designing complex automata efficiently.
• Applications of ε-NFAs include simplifying the design of pattern recognizers and regular expressions.