Finite Automata
Finite Automata (FA) are simple computational models that help us understand how machines process strings of input. They are used to recognise specific patterns in data and are fundamental in the study of computation and formal languages.
Key Components of Finite Automata
Finite Automata consist of the following essential components:
- States (Q): These are the different conditions or configurations that the automaton can be in.
- Alphabet (Σ): A set of symbols that the automaton can recognize as inputs.
- Transition Function (δ): Rules that define how the automaton moves from one state to another based on the current state and input symbol.
- Start State (q₀): The state where the automaton begins its processing.
- Accept States (F): These are specific states that indicate the input string is accepted if the automaton ends in one of them.
Types of Finite Automata
There are two primary types of Finite Automata:
- Deterministic Finite Automata (DFA): In a DFA, for each state and input symbol, there is exactly one possible next state. It provides a clear and predictable behavior for recognizing patterns.
- Non-Deterministic Finite Automata (NFA): In an NFA, for a given state and input symbol, there can be multiple possible transitions or even none. Despite this flexibility, NFAs are computationally equivalent to DFAs.
Formal Definition
A Finite Automaton is formally defined as a 5-tuple (Q, Σ, δ, q₀, F), where:
- Q: A finite set of states.
- Σ: A finite set of input symbols, also known as the alphabet.
- δ: The transition function, which maps (state, input) pairs to a next state.
- q₀: The start state, which belongs to Q.
- F: A subset of Q that contains the accept states.
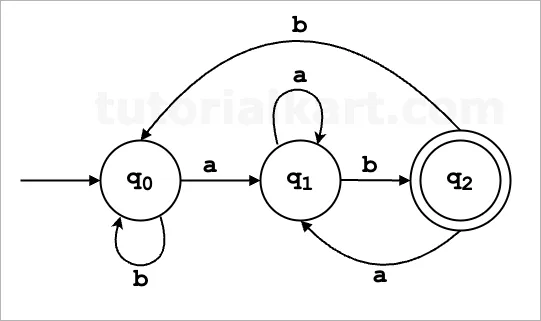
Example: DFA for Strings Ending with ‘ab’
Let’s create a DFA to recognise strings over the alphabet Σ = {a, b} that end with the substring ‘ab’.
We need to construct a Deterministic Finite Automaton (DFA) to recognize strings over the alphabet Σ = {a, b} that end with the substring ‘ab’. A string is considered accepted if it ends with this specific pattern, regardless of its prefix. For example:
- Accepted Strings:
'ab','aab','bab','aaab','bbbab' - Rejected Strings:
'a','b','ba','aaa','bba'
The DFA must correctly handle:
- Start state: Where the computation begins.
- Transitions: Moves between states based on the input character.
- Accept state: Where the DFA ends if the string is valid.
Components of the DFA
States, Q: {q₀, q₁, q₂}
- q₀: Initial state. Represents the scenario where no part of the target substring ‘ab’ has been detected yet.
- q₁: Intermediate state. Represents that the input has ended with ‘a’ but not yet formed the ‘ab’ substring.
- q₂: Accept state. Represents that the input ends with ‘ab’, making the string valid.
Alphabets which are Input, Σ: {a, b}
- The set of characters the DFA can read: Σ = {a, b}.
Start State (q₀):
- The state where the DFA begins processing.
Accept State F: {q₂}
- q₂: The state where the DFA ends if the input string ends with
'ab'.
Transition Rules (δ):
These rules define how the DFA moves between states based on the input:
δ(q₀, 'a') = q₁
δ(q₁, 'b') = q₂
δ(q₂, 'a') = q₁
δ(q₂, 'b') = q₀
δ(q₀, 'b') = q₀
δ(q₁, 'a') = q₁δ(q₀, 'a') = q₁: Transition from q₀ to q₁ on seeing ‘a’.δ(q₁, 'b') = q₂: Transition from q₁ to q₂ on seeing ‘b’ (completes ‘ab’).δ(q₂, 'a') = q₁: Transition from q₂ to q₁ on seeing ‘a’ (potential new ‘ab’ start).δ(q₂, 'b') = q₀: Transition from q₂ to q₀ on seeing ‘b’ (reset; no ‘ab’).δ(q₀, 'b') = q₀: Stay in q₀ on seeing ‘b’ (no ‘ab’ possible yet).δ(q₁, 'a') = q₁: Stay in q₁ on seeing ‘a’ (waiting for ‘b’).
State Diagram