Nondeterministic Finite Automata (NFA)
A Nondeterministic Finite Automaton (NFA) is a type of finite automaton where multiple transitions are allowed for a given state and input symbol. In some cases, there may even be transitions without any input symbol (ε-transitions). NFAs are flexible and easier to construct than their deterministic counterparts, though they are computationally equivalent to DFAs.
Key Features of NFA
NFAs have the following characteristics:
- Multiple Transitions: For a given state and input symbol, an NFA can transition to multiple next states.
- ε-Transitions: An NFA can transition from one state to another without consuming any input symbol.
- Acceptance: An NFA accepts a string if there exists at least one sequence of transitions that ends in an accept state after processing the input.
- Non-Determinism: Unlike DFAs, the behavior of an NFA is not predictable at each step as it may have multiple choices for transitions.
Formal Definition
An NFA is formally defined as a 5-tuple (Q, Σ, δ, q₀, F), where:
- Q: A finite set of states.
- Σ: A finite input alphabet.
- δ: A transition function, δ: Q × (Σ ∪ {ε}) → 2^Q, which maps a state and input symbol (or ε) to a set of next states.
- q₀: The start state, where the NFA begins processing.
- F: A set of accept states, F ⊆ Q.
Example: NFA for Strings Ending with ‘ab’
Let’s create an NFA to recognize strings over the alphabet Σ = {a, b} that end with the substring ‘ab’.
We need to construct a Nondeterministic Finite Automaton (NFA) to recognize strings that end with the substring ‘ab’. The key difference from a DFA is that an NFA allows multiple transitions for the same input from a given state, and acceptance is determined if any computation path leads to an accept state. For example:
- Accepted Strings:
'ab','aab','bab','aaab','bbbab' - Rejected Strings:
'a','b','ba','aaa','bba'
Components of the NFA
States, Q: {q₀, q₁, q₂}
- q₀: Initial state. Represents the scenario where no part of the target substring ‘ab’ has been detected yet.
- q₁: Intermediate state. Represents that the input has ended with ‘a’ but not yet formed the ‘ab’ substring.
- q₂: Accept state. Represents that the input ends with ‘ab’, making the string valid.
Alphabets which are Input, Σ: {a, b}
- The set of characters the NFA can read: Σ = {a, b}.
Start State (q₀):
- The state where the NFA begins processing.
Accept State F: {q₂}
- q₂: The state where the NFA ends if the input string contains
'ab'.
Transition Rules (δ):
These rules define how the NFA moves between states based on the input:
δ(q₀, 'a') = {q₀, q₁}
δ(q₀, 'b') = {q₀}
δ(q₁, 'b') = {q₂}
δ(q₁, 'a') = {}
δ(q₂, 'a') = {}
δ(q₂, 'b') = {}δ(q₀, 'a') = {q₀, q₁}: On input ‘a’, the NFA can stay in q₀ or move to q₁.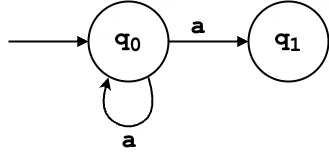
δ(q₀, 'b') = {q₀}: On input ‘b’, the NFA stays in q₀.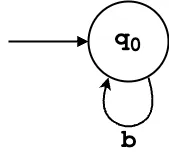
δ(q₁, 'b') = {q₂}: On input ‘b’, the NFA moves to q₂, completing ‘ab’.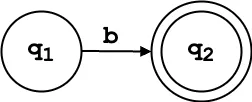
δ(q₁, 'a') = {}: On input ‘a’, the NFA cannot transition further from q₁.δ(q₂, 'a') = {}: On input ‘a’, the NFA cannot transition further from q₂.δ(q₂, 'b') = {}: On input ‘b’, the NFA cannot transition further from q₂.
State Diagram
By combining all the above transitions, we get the following state diagram.
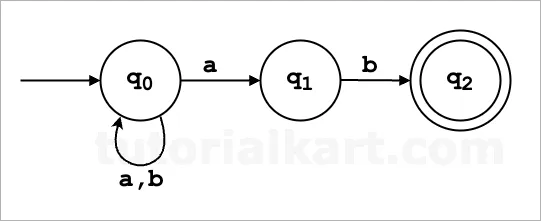
Key Takeaways
- NFAs allow multiple transitions for a given input and can include ε-transitions.
- They are easier to construct than DFAs, especially for complex patterns.
- NFAs and DFAs are computationally equivalent, meaning every NFA has an equivalent DFA that recognizes the same language.
- NFAs are commonly used in the implementation of regular expressions and text searching algorithms.
