Regular Expressions

A Regular Expression (regex or regexp) is a formal language notation used to define patterns in strings. Regular expressions are widely used in computer science for tasks like pattern matching, text searching, and defining regular languages. They are directly equivalent to finite automata, which makes them a key concept in automata theory.

Syntax of Regular Expressions

The syntax of regular expressions defines how patterns are expressed. Below are the main components:

Alphabet Symbols: Individual characters from the input alphabet (e.g., ‘a’, ‘b’, ‘0’, ‘1’).
Concatenation: Writing two expressions next to each other signifies their sequence. For example, ab matches “a” followed by “b”.
Union: Represented by the pipe symbol |. For example, a|b matches either “a” or “b”.
Kleene Star: Represented by *, it denotes zero or more repetitions of a pattern. For example, a* matches “”, “a”, “aa”, and so on.
Parentheses: Used to group expressions for clarity and precedence. For example, (a|b)c matches “ac” or “bc”.

Operations on Regular Expressions

Regular expressions support three fundamental operations:

Union: Combines two patterns such that either can match. For example, a|b matches “a” or “b”.
Concatenation: Matches sequences of patterns. For example, ab matches “a” followed by “b”.
Kleene Star: Allows repetition of a pattern. For example, a* matches “”, “a”, “aa”, “aaa”, and so on.

These operations form the basis for defining all regular languages, making regular expressions a powerful tool for describing patterns.

Equivalence with Finite Automata

Regular expressions and finite automata are equivalent in their expressive power. This means that for every regular expression, there exists a finite automaton (DFA or NFA) that recognizes the same language, and vice versa.

The equivalence is established through the following:

From Regular Expression to NFA: Using a method called Thompson’s construction, an NFA can be constructed for any given regular expression.
From NFA to DFA: Using the subset construction method, an NFA can be converted to an equivalent DFA.
From DFA to Regular Expression: Techniques like state elimination can be used to derive a regular expression from a DFA.

This equivalence highlights the theoretical foundation of regular expressions and their practical use in defining and recognizing regular languages.

Example: Regular Expression and Equivalent NFA

Let’s construct an NFA for the regular expression (a|b)*ab, which matches any string of ‘a’s and ‘b’s that ends with “ab”.

The regular expression can be broken into two parts:

(a|b)*: Matches any sequence of ‘a’s and ‘b’s, including the empty string.
ab: Ensures that the string ends with the exact sequence “ab”.

We will construct an NFA for this regular expression using Thompson’s construction method.

Step 1: Construct NFA for Each Component

To construct the NFA, we break the regular expression into its components and build NFAs for each part:

For (a|b): Create two parallel transitions from a state, one for ‘a’ and another for ‘b’.
For (a|b)*: Add a loop to handle repetition, allowing the NFA to return to the starting state after reading ‘a’ or ‘b’.
For ab: Add two sequential transitions: one for ‘a’, then another for ‘b’.

Step 2: Combine NFAs

Next, we combine the NFAs for each part:

Connect the NFA for (a|b)* to the start of the NFA for ab.
Ensure the final state of the NFA for ab is the accept state for the combined NFA.
Include ε-transitions where necessary to combine the components seamlessly.

Step 3: Define the NFA

The resulting NFA has the following components:

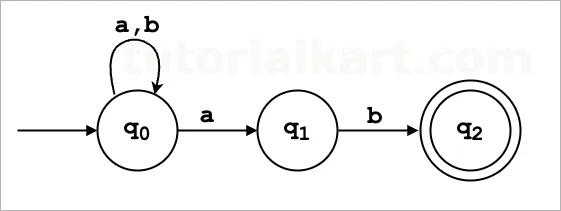
States (Q): q₀, q₁, q₂

Alphabet (Σ): {a, b}

Start State: q₀

Accept State: q₂

Transition Function (δ):

δ(q₀, 'a') = {q₀, q₁}
δ(q₀, 'b') = {q₀}
δ(q₁, 'b') = {q₂}
δ(q₁, 'a') = {}
δ(q₂, 'a') = {}
δ(q₂, 'b') = {}

Key Transitions:

q₀: Handles repetition of ‘a’ and ‘b’ for (a|b)*.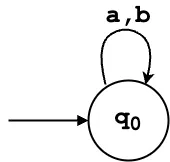
q₁: Transition for the first ‘a’ in “ab”.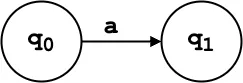
q₂: Accept state reached after “ab”.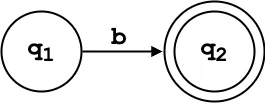

State Diagram

State diagram showing all transitions for ‘a’, ‘b’, and ε, with q₀ as the start state and q₂ as the accept state.

Key Takeaways

Regular expressions are a concise and powerful way to describe patterns in strings.
They support operations like union, concatenation, and Kleene star to define regular languages.
Regular expressions are equivalent to finite automata, providing a bridge between formal language theory and practical applications like pattern matching and lexical analysis.
Understanding their syntax, operations, and equivalence with finite automata is essential for mastering computational theory.

TutorialKart

Regular Expressions