Go – Armstrong Number
In this tutorial, we will learn how to check if a number is an Armstrong number using the Go programming language (Golang). We will explain the concept of an Armstrong number, provide a detailed algorithm, and write a program to determine whether a given number is an Armstrong number.
What is an Armstrong Number?
An Armstrong number (or Narcissistic number) is a number that is equal to the sum of its own digits each raised to the power of the number of digits. For example:
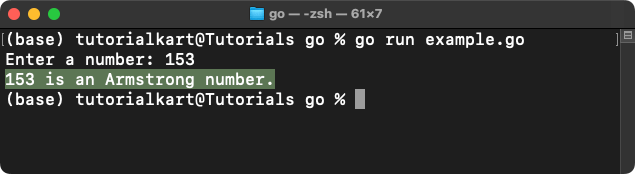
- 153: \( 1^3 + 5^3 + 3^3 = 153 \) (Armstrong number)
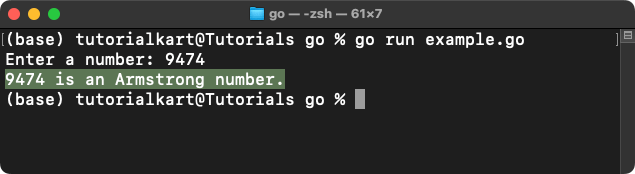
- 9474: \( 9^4 + 4^4 + 7^4 + 4^4 = 9474 \) (Armstrong number)
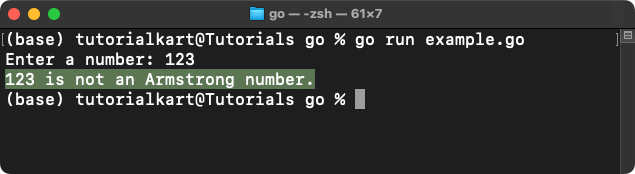
- 123: \( 1^3 + 2^3 + 3^3 = 36 \) (Not an Armstrong number)
Logic to Check Armstrong Number
The steps to determine whether a number is an Armstrong number are as follows:
- Find the number of digits in the number (denoted as
n). - Separate the digits of the number.
- Raise each digit to the power of
nand sum the results. - Compare the sum with the original number. If they are equal, the number is an Armstrong number.
Example Program to Check Armstrong Number
Program – example.go
</>
Copy
package main
import (
"fmt"
"math"
)
func isArmstrong(number int) bool {
original := number
sum := 0
digits := 0
// Calculate the number of digits
temp := number
for temp != 0 {
digits++
temp /= 10
}
// Calculate the sum of each digit raised to the power of digits
temp = number
for temp != 0 {
digit := temp % 10
sum += int(math.Pow(float64(digit), float64(digits)))
temp /= 10
}
// Check if the sum is equal to the original number
return sum == original
}
func main() {
// Input number
var num int
fmt.Print("Enter a number: ")
fmt.Scan(&num)
// Check and display result
if isArmstrong(num) {
fmt.Println(num, "is an Armstrong number.")
} else {
fmt.Println(num, "is not an Armstrong number.")
}
}Explanation of Program
- Calculate the number of digits: – A temporary variable (
temp) is used to count the digits by repeatedly dividing the number by 10. - Compute the sum: – Each digit is extracted using the modulus operator (
%), raised to the power of the number of digits using themath.Powfunction, and added to a running total (sum). - Check the Armstrong condition: – The computed
sumis compared to the original number. - Output the result: – The result is printed, indicating whether the input number is an Armstrong number or not.
Output