Karnaugh Maps (K-Maps) are essential tools in digital electronics for simplifying Boolean expressions. They provide a graphical method to minimize logic functions, making circuit design more efficient. This guide will take you through 2-variable, 3-variable, 4-variable, and 5-variable Karnaugh Maps, offering visualizations and step-by-step instructions for each.
What is a Karnaugh Map (K-Map)?
A Karnaugh Map is a grid-based representation of a truth table. It helps in identifying adjacent minterms that can be grouped together, leading to a simplified Boolean expression.
Each K-Map is structured based on the number of input variables:
- 2 Variables: 4 cells
- 3 Variables: 8 cells
- 4 Variables: 16 cells
- 5 Variables: 32 cells (divided into two 4-variable maps)
2-Variable Karnaugh Map
A 2-variable K-Map simplifies Boolean expressions involving two input variables, AA and BB. It consists of 4 cells, representing all possible combinations of AA and BB.
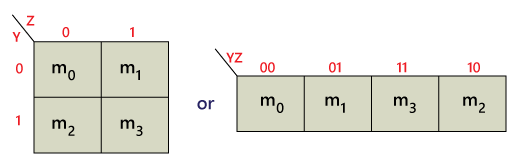
K-Map Layout:
| A\B | 0 | 1 |
|---|---|---|
| 0 | m0 | m1 |
| 1 | m2 | m3 |
Steps to Use:
- Fill the cells with the output values from the truth table.
- Group adjacent cells with 1s (horizontally or vertically).
- Write the simplified expression.
Example:
Function: F(A,B)=AB+A′B′F(A, B) = AB + A’B’
K-Map:
| A\B | 0 | 1 |
|---|---|---|
| 0 | 1 | 0 |
| 1 | 0 | 1 |
Simplified Expression: F=A⋅B+A′⋅B′F = A \cdot B + A’ \cdot B’
3-Variable Karnaugh Map
A 3-variable K-Map involves three inputs: AA, BB, and CC. It consists of 8 cells, representing all combinations of these variables.
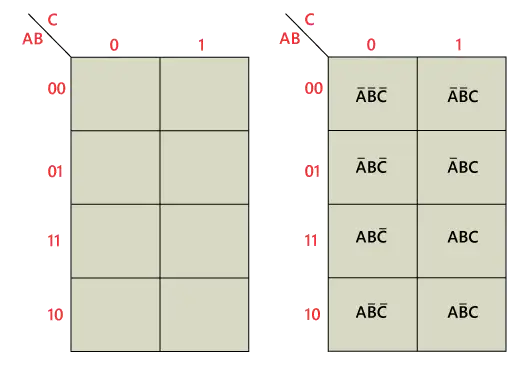
K-Map Layout:
| AB\C | 0 | 1 |
|---|---|---|
| 00 | m0 | m1 |
| 01 | m2 | m3 |
| 11 | m6 | m7 |
| 10 | m4 | m5 |
Steps to Use:
- Fill the cells with output values.
- Identify adjacent cells with 1s.
- Group these cells to form simplified terms.
Example:
Function: F(A,B,C)=AB+A′CF(A, B, C) = AB + A’C
K-Map:
| AB\C | 0 | 1 |
|---|---|---|
| 00 | 0 | 1 |
| 01 | 0 | 1 |
| 11 | 1 | 1 |
| 10 | 1 | 1 |
Simplified Expression: F=A+CF = A + C
4-Variable Karnaugh Map
A 4-variable K-Map includes four inputs: AA, BB, CC, and DD. It consists of 16 cells, representing all combinations of these variables.
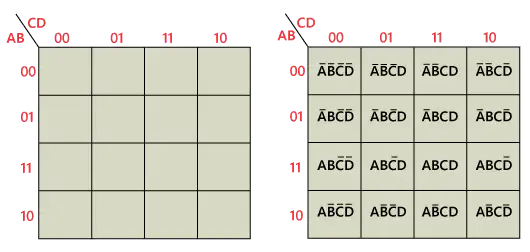
K-Map Layout:
| AB\CD | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | m0 | m1 | m3 | m2 |
| 01 | m4 | m5 | m7 | m6 |
| 11 | m12 | m13 | m15 | m14 |
| 10 | m8 | m9 | m11 | m10 |
Steps to Use:
- Fill the cells with output values.
- Group adjacent cells with 1s in groups of 1,2,4,81, 2, 4, 8, or 1616.
- Write the simplified expression.
Example:
Function: F(A,B,C,D)=A′B′C′D+AB′C′D′F(A, B, C, D) = A’B’C’D + AB’C’D’
K-Map:
| AB\CD | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | 1 | 0 | 0 | 0 |
| 01 | 0 | 0 | 0 | 0 |
| 11 | 0 | 0 | 0 | 0 |
| 10 | 0 | 1 | 0 | 0 |
Simplified Expression: F=A′B′C′D+AB′C′D′F = A’B’C’D + AB’C’D’
5-Variable Karnaugh Map
A 5-variable K-Map extends the 4-variable K-Map by splitting it into two grids, one for each value of the 5th variable (E=0E = 0 and E=1E = 1).
K-Map Layout:
Map 0 (E=0) and Map 1 (E=1):
| AB\CD | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | m0 | m1 | m3 | m2 |
| 01 | m4 | m5 | m7 | m6 |
| 11 | m12 | m13 | m15 | m14 |
| 10 | m8 | m9 | m11 | m10 |
Steps to Use:
- Place output values in Map 0 and Map 1 based on EE.
- Group adjacent cells with 1s across both maps.
- Write the simplified Boolean expression.
Example:
Function: F(A,B,C,D,E)F(A, B, C, D, E)
| Map 0 (E=0) | Map 1 (E=1) |
|---|---|
| Filled values | Filled values |
Simplified Expression: Combine groups from both maps.
Conclusion
Karnaugh Maps simplify Boolean expressions for 2 to 5 variables, reducing logic complexity and optimizing circuit design. By mastering these tools, you can efficiently tackle combinational logic problems in digital electronics. For more advanced designs, 5-variable K-Maps provide a practical extension to handle complex functions.
Let me know if you need help with specific examples or additional diagrams!
