Random Forest in Machine Learning
Random Forest in Machine Learning is a method for classification(classifying an experiment to a category), or regression(predicting the outcome of an experiment), based on the training data(knowledge of previous experiments). Random forest handles non-linearity by exploiting correlation between the features of data-point/experiment.
With training data, that has correlations between the features, Random Forest method is a better choice for classification or regression. Generally stating,
Random forest is opted for tasks that include generating multiple decision trees during training and considering the outcome of polls of these decision trees, for an experiment/data-point, as prediction.
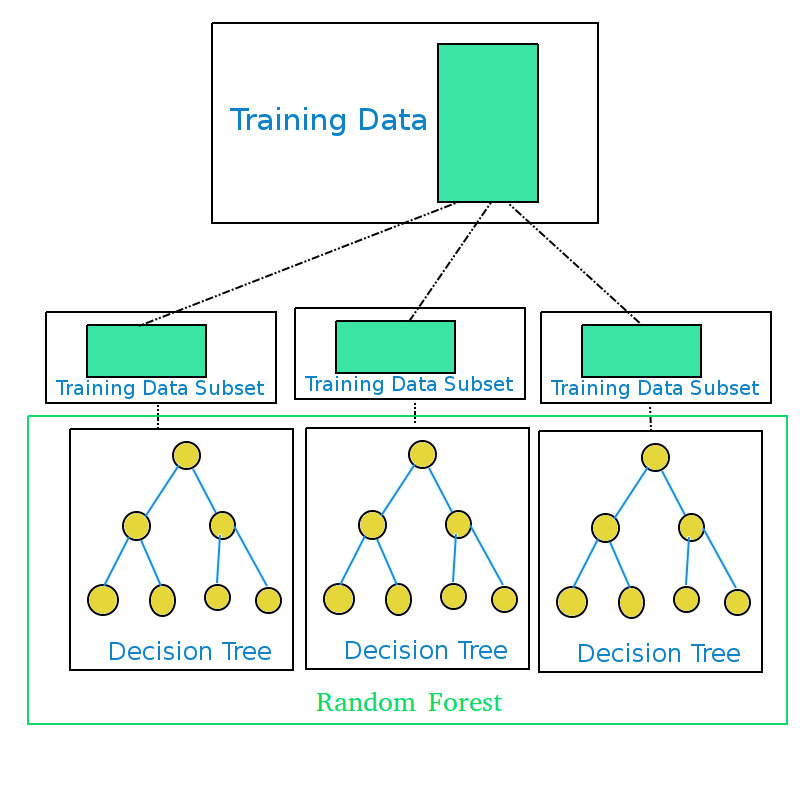
Random Decision Forest/Random Forest is a group of decision trees.Decision tree is the base learner in a Random forest. The decision trees are grown by feeding on training data.
A decision tree has a disadvantage of over-fitting the model to the training data. Random forest overcomes this disadvantage with a lot of decision trees. All these decision trees, in the Random Forest, do polling during the prediction and majority of the polls is considered, the result of prediction. This polling from multiple decision trees eliminates any over-fitting of some decision trees to the training data .
A model of Random forest comprises of the following:
- Decision trees that are grown using training data
- Features recognized/used for the modeling of the data
To make a note, Random Forests(tm) is a trademark of Leo Breiman and Adele Cutler with the official site https://www.stat.berkeley.edu/~breiman/RandomForests/cc_home.htm
How Decision Trees are grown in Random Forest?
- Get the training data
- Split the training data into subsets randomly. (Number of subsets should be equal to the number of decision trees to be grown)
- Generate a decision tree for each training data subset.
- Ensemble of the decision trees generated is the Random Forest.
What is the training data for a Random Forest in Machine Learning ?
Training data is an array of vectors in the N-dimension space. Each dimension in the space corresponds to a feature that you have recognized from the data, wherefore there are N features that you have recognized from the nature of data to model. In other words, each vector is composed of multiple unit vectors, not necessarily all the independent unit vectors. And, each unit vector corresponds to a feature. When data points of training data is expressed mathematically:
| C1 : V1f1 + V2f2 + V3f3 + . . . . . + Vifi + . . . VNfN |
| C2 : Vector |
| C1 : Vector |
| . . . |
| CM : Vector |
where Vi is the value of the feature fi, for the data point that corresponds to Category Cj.
If you observe the table, there would be multiple vectors corresponding to a Category.
What is the data for a Random Forest Model to predict?
The problem instance which is a N-dimensional feature vector, similar to feature vectors that are used for training. It is important that the feature vector that has come for prediction also contain all the feature values as that of in training.
| Ck : V1f1 + V2f2 + V3f3 + . . . . . + Vifi + . . . VNfN |
Sometimes, the data point may not have some of the features, in that case their value is zero. In terms of vector, the weight of the unit vector corresponding to those features is zero.
Feature correlations/interactions to handle non-linearity
When fitting the model for the responses of a non-linear machine and the features selected, Random forest handles non-linearity by performing branch specific splits. When a split happens at an i-th branch, it is meant that a combination/interaction of i independent features is considered already, which is the feature interaction.
Conclusion
In this machine learning tutorial, we have learnt how a Random Forest in Machine Learning is useful, constructing a Random Forest with Decision Trees, and exploiting the relations between features.