Arc Length of a Circle Formula
The arc length of a circle is the distance along a section of the circumference, between two points on the circle. The arc length depends on the radius or diameter of the circle and the angle subtended by the arc at the circle’s center.
In the following figure, arc is highlighted in blue color.
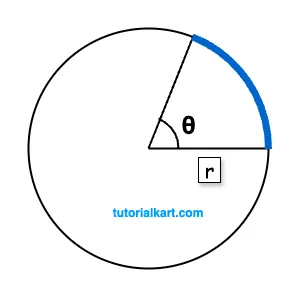
In this guide, we go through the formulas for calculating the arc length of a circle, with detailed explanations and examples for each method.
Formulas for the Arc Length of a Circle
Using Radius and Angle in Degrees:
If the radius \( r \) of the circle and the central angle \( \theta \) (in degrees) are known, the arc length \( L \) can be calculated with the formula:
\( L = \dfrac{\theta}{360} \times 2 \pi r \)
Using Radius and Angle in Radians:
If the radius \( r \) and the central angle \( \theta \) (in radians) are known, the arc length \( L \) can be calculated as:
\( L = r \theta \)
Using Diameter and Angle in Degrees:
If the diameter \( d \) of the circle and the central angle \( \theta \) (in degrees) are known, the arc length \( L \) can be calculated as:
\( L = \dfrac{\theta}{360} \times \pi d \)
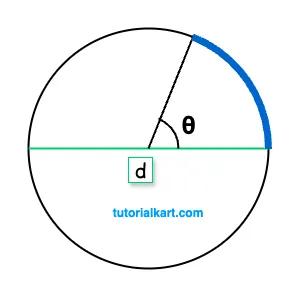
In these formulas:
- \( r \) is the radius of the circle
- \( d \) is the diameter of the circle, where \( d = 2r \)
- \( \theta \) is the central angle in degrees or radians
- \( \pi \) (Pi) is approximately equal to 3.14159
Detailed Explanation of Each Formula
1 Formula for Arc Length Using Radius and Angle in Degrees
The formula \( L = \dfrac{\theta}{360} \times 2 \pi r \) calculates the arc length by taking a fraction of the circumference based on the angle in degrees. This formula is commonly used when the radius and central angle in degrees are known.
Example 1: Calculating Arc Length with Radius and Angle in Degrees
Problem: Find the arc length of a circle with radius \( r = 7 \, \text{cm} \) and a central angle of \( \theta = 60^\circ \).
Solution:
- Write down the formula: \( L = \dfrac{\theta}{360} \times 2 \pi r \).
- Substitute \( r = 7 \) and \( \theta = 60 \): \( L = \dfrac{60}{360} \times 2 \pi \times 7 \).
- Simplify the fraction: \( L = \dfrac{1}{6} \times 2 \pi \times 7 \).
- Multiply: \( L = \dfrac{14\pi}{6} \approx 7.33 \, \text{cm} \) (using \( \pi \approx 3.14159 \)).
The arc length is approximately \( 7.33 \, \text{cm} \).
2 Formula for Arc Length Using Radius and Angle in Radians
The formula \( L = r \theta \) calculates the arc length directly using the radius and the angle in radians. This method is useful when the angle is given in radians.
Example 2: Calculating Arc Length with Radius and Angle in Radians
Problem: A circle has a radius of \( r = 5 \, \text{cm} \) and a central angle of \( \theta = 1.2 \) radians. Find the arc length.
Solution:
- Write down the formula: \( L = r \theta \).
- Substitute \( r = 5 \) and \( \theta = 1.2 \): \( L = 5 \times 1.2 \).
- Multiply: \( L = 6 \, \text{cm} \).
The arc length is \( 6 \, \text{cm} \).
3 Formula for Arc Length Using Diameter and Angle in Degrees
The formula \( L = \dfrac{\theta}{360} \times \pi d \) calculates the arc length by taking a fraction of the circumference based on the angle in degrees. This form is convenient when the diameter and the central angle in degrees are known.
Example 3: Calculating Arc Length with Diameter and Angle in Degrees
Problem: A circle has a diameter of \( d = 12 \, \text{cm} \) and a central angle of \( \theta = 90^\circ \). Find the arc length.
Solution:
- Write down the formula: \( L = \dfrac{\theta}{360} \times \pi d \).
- Substitute \( d = 12 \) and \( \theta = 90 \): \( L = \dfrac{90}{360} \times \pi \times 12 \).
- Simplify the fraction: \( L = \dfrac{1}{4} \times \pi \times 12 \).
- Multiply: \( L = 3\pi \approx 9.42 \, \text{cm} \) (using \( \pi \approx 3.14159 \)).
The arc length is approximately \( 9.42 \, \text{cm} \).
These examples demonstrate how to calculate the arc length of a circle using different measurements, whether it’s the radius and angle in degrees or radians, or the diameter and angle in degrees.
