Formula for Area of a Rectangle – Detailed Explanation and Examples

Area of a Rectangle Formula

The area of a rectangle is the measure of space enclosed within its four sides. A rectangle has opposite sides that are equal in length, and each interior angle is 90 degrees.

Calculating the area of a rectangle is straightforward and can be done using either the length and width or, in some cases, the length and diagonal.

Below are the two formulas for calculating the area of a rectangle, with detailed explanations and examples for each method.

Formulas for the Area of a Rectangle

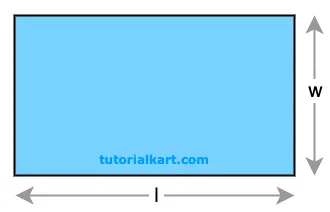
Using Length and Width:

If the length \( l \) and width \( w \) of the rectangle are known,

The area \( A \) can be calculated with the formula:

\( A = l \times w \)

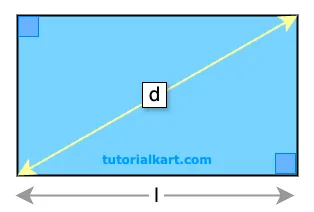
Using Length and Diagonal:

If the length \( l \) and the diagonal \( d \) of the rectangle are known,

The area \( A \) can be calculated as:

\( A = l \times \sqrt{d^2 – l^2} \)

In these formulas:

• \( l \) is the length of the rectangle
• \( w \) is the width of the rectangle
• \( d \) is the diagonal of the rectangle, where \( d = \sqrt{l^2 + w^2} \)

---

Detailed Explanation of Each Formula

---

1. Formula for Area of a Rectangle Using Length and Width

The formula \( A = l \times w \) calculates the area of a rectangle by multiplying the length by the width.

This is the most straightforward way to find the area when both the length and width are known.

Example 1: Calculating Area with Given Length and Width

Problem: Find the area of a rectangle with a length of \( l = 10 \, \text{cm} \) and a width of \( w = 5 \, \text{cm} \).

Solution:

1. Write down the formula: \( A = l \times w \).
2. Substitute \( l = 10 \) and \( w = 5 \): \( A = 10 \times 5 \).
3. Multiply: \( A = 50 \, \text{cm}^2 \).

The area of the rectangle is \( 50 \, \text{cm}^2 \).

---

2. Formula for Area of a Rectangle Using Length and Diagonal

The formula \( A = l \times \sqrt{d^2 – l^2} \) calculates the area of a rectangle by using the length and diagonal. This method is useful when the diagonal and one side length are known.

Since the diagonal forms a right triangle with the length and width, the width can be found as \( w = \sqrt{d^2 – l^2} \) and then used to calculate the area.

Example 2: Calculating Area with Given Length and Diagonal

Problem: A rectangle has a length of \( l = 8 \, \text{cm} \) and a diagonal of \( d = 10 \, \text{cm} \). Find the area.

Solution:

1. Write down the formula: \( A = l \times \sqrt{d^2 – l^2} \).
2. Substitute \( l = 8 \) and \( d = 10 \): \( A = 8 \times \sqrt{10^2 – 8^2} \).
3. Calculate inside the square root: \( A = 8 \times \sqrt{100 – 64} = 8 \times \sqrt{36} \).
4. Find the square root: \( A = 8 \times 6 = 48 \, \text{cm}^2 \).

The area of the rectangle is \( 48 \, \text{cm}^2 \).

These examples demonstrate how to calculate the area of a rectangle using either the length and width or the length and diagonal, depending on the available measurements.