Area of a Circle Formula
The area of a circle represents the space enclosed within its boundary.
You can calculate the area using either the radius (distance from the center to the edge) or the diameter (distance across the circle through the center).
The following are the formulas for calculating the area of a circle, along with detailed explanations and examples for each.
Formulas for the Area of a Circle
Using Radius:
If the radius \( r \) of the circle is known, the area \( A \) can be calculated with the formula:
\( A = \pi r^2 \)
Using Diameter:
If the diameter \( d \) of the circle is known, the area \( A \) can be calculated as:
\( A = \dfrac{\pi d^2}{4} \)
Detailed Explanation of Each Formula
1 Area of a Circle using Radius
The formula \( A = \pi r^2 \) calculates the area of a circle by squaring the radius and multiplying by \( \pi \), which represents the ratio of a circle’s circumference to its diameter (approximately 3.14159).
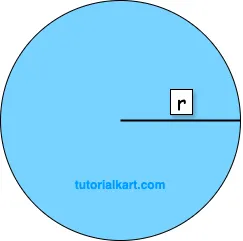
This formula is derived from the relationship between the radius and the entire area enclosed by the circle. This form is used when the radius is directly provided or easily measured.
Example 1: Calculating Area with a Given Radius
Problem: Find the area of a circle with a radius of \( r = 5 \, \text{cm} \).
Solution:
- Use the formula \( A = \pi r^2 \).
- Substitute \( r = 5 \): \( A = \pi \times 5^2 \).
- Calculate the square of the radius: \( A = \pi \times 25 \).
- Multiply by \( \pi \): \( A = 25\pi \approx 78.54 \, \text{cm}^2 \) (using \( \pi \approx 3.14159 \)).
The area of the circle is approximately \( 78.54 \, \text{cm}^2 \).
Example 2: Finding Radius from the Area
Problem: The area of a circle is given as \( 50 \, \text{cm}^2 \). What is the radius?
Solution:
- Start with the formula \( A = \pi r^2 \).
- Set \( A = 50 \) and solve for \( r \): \( 50 = \pi r^2 \).
- Divide both sides by \( \pi \): \( r^2 = \dfrac{50}{\pi} \).
- Approximate \( \pi \approx 3.14159 \): \( r^2 = \dfrac{50}{3.14159} \approx 15.92 \).
- Take the square root of both sides to find \( r \): \( r \approx \sqrt{15.92} \approx 3.99 \, \text{cm} \).
The radius of the circle is approximately \( 3.99 \, \text{cm} \).
2 Area of a Circle using Diameter
When the diameter \( d \) of a circle is known, you can calculate the area with the formula
\( A = \dfrac{\pi d^2}{4} \).
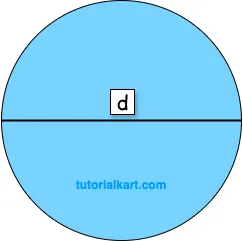
This formula is derived from the radius-based formula, since \( r = \dfrac{d}{2} \). By substituting \( r = \dfrac{d}{2} \) into \( A = \pi r^2 \), we get \( A = \pi \left(\dfrac{d}{2}\right)^2 = \dfrac{\pi d^2}{4} \). This form is convenient when only the diameter is measured or known.
Example 3: Calculating Area with a Given Diameter
Problem: A circle has a diameter of \( d = 10 \, \text{cm} \). Find the area.
Solution:
- Use the formula \( A = \dfrac{\pi d^2}{4} \).
- Substitute \( d = 10 \): \( A = \dfrac{\pi \times 10^2}{4} \).
- Calculate the square of the diameter: \( A = \dfrac{\pi \times 100}{4} \).
- Simplify: \( A = 25\pi \approx 78.54 \, \text{cm}^2 \).
The area of the circle with a diameter of \( 10 \, \text{cm} \) is approximately \( 78.54 \, \text{cm}^2 \).
Example 4: Solving for Area in Terms of Pi with Diameter
Problem: A circle has a diameter of \( d = 14 \, \text{cm} \). Find the area in terms of \( \pi \).
Solution:
- Use the formula \( A = \dfrac{\pi d^2}{4} \).
- Substitute \( d = 14 \): \( A = \dfrac{\pi \times 14^2}{4} \).
- Calculate the square of the diameter: \( A = \dfrac{\pi \times 196}{4} \).
- Simplify: \( A = 49\pi \, \text{cm}^2 \).
The area of the circle is \( 49\pi \, \text{cm}^2 \) in terms of \( \pi \).
Conclusion
These examples illustrate the use of both forms of the area formula. You can choose the one most suitable for the given measurements, whether the radius or diameter is known.
