Area of a Parallelogram Formula
The area of a parallelogram is the measure of the space enclosed within its four sides. In a parallelogram, opposite sides are equal and parallel, and opposite angles are equal.

There are several ways to calculate the area depending on the given information, such as base and height or two adjacent sides and the angle between them.
Below are two formulas for calculating the area of a parallelogram, with detailed explanations and examples for each.
Formulas for the Area of a Parallelogram
Using Base and Height:
When the base and the perpendicular height are known, the area \( A \) of a parallelogram is given by:
\( A = \text{base} \times \text{height} \)
Using Two Sides and the Included Angle:
When the lengths of two adjacent sides and the angle between them are known, the area \( A \) of the parallelogram is calculated by:
\( A = a \times b \times \sin(\theta) \)
In these formulas:
- \( \text{base} \) is the length of the base of the parallelogram
- \( \text{height} \) is the perpendicular distance from the base to the opposite side
- \( a \) and \( b \) are the lengths of two adjacent sides
- \( \theta \) is the angle between the sides \( a \) and \( b \)
Detailed Explanation of Each Formula
1 Area of a Parallelogram using Base and Height
The formula \( A = \text{base} \times \text{height} \) calculates the area of a parallelogram by multiplying the base by the perpendicular height.
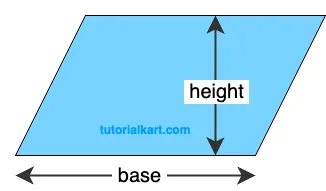
This form is used when the base and the perpendicular height from that base to the opposite side are known.
Example 1: Calculating Area of a Parallelogram with a Given Base and Height
Problem: Find the area of a parallelogram with a base of \( 8 \, \text{cm} \) and a height of \( 5 \, \text{cm} \).
Solution:
- Write down the formula: \( A = \text{base} \times \text{height} \).
- Substitute the given values: \( A = 8 \times 5 \).
- Multiply the base and height: \( A = 40 \, \text{cm}^2 \).
The area of the parallelogram is \( 40 \, \text{cm}^2 \).
2 Area of a Parallelogram using Two Sides and the Included Angle
The formula \( A = a \times b \times \sin(\theta) \) calculates the area of a parallelogram by multiplying the lengths of two adjacent sides and then multiplying by the sine of the angle between them.
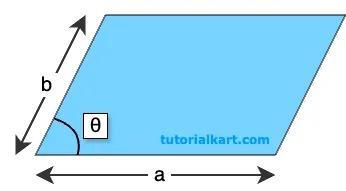
This form is useful when the base and the adjacent side lengths are known, along with the included angle.
Example 2: Calculating Area of a Parallelogram with Given Sides and Angle
Problem: A parallelogram has two adjacent sides, \( a = 6 \, \text{cm} \) and \( b = 10 \, \text{cm} \), with an angle \( \theta = 45^\circ \) between them. Find the area of the parallelogram.
Solution:
- Write down the formula: \( A = a \times b \times \sin(\theta) \).
- Substitute the given values: \( A = 6 \times 10 \times \sin(45^\circ) \).
- Use \( \sin(45^\circ) = \dfrac{\sqrt{2}}{2} \): \( A = 6 \times 10 \times \dfrac{\sqrt{2}}{2} \).
- Simplify: \( A = 30\sqrt{2} \approx 42.43 \, \text{cm}^2 \).
The area of the parallelogram is approximately \( 42.43 \, \text{cm}^2 \).
These examples demonstrate how to calculate the area of a parallelogram depending on the measurements provided, whether it’s the base and height or the lengths of adjacent sides with the included angle.
