Formula for Area of a Rhombus – Detailed Explanation and Examples

Area of a Rhombus Formula

The area of a rhombus is the space enclosed within its four equal sides. A rhombus is a special type of parallelogram where all four sides are equal, and its opposite angles are equal. You can calculate the area of a rhombus using different formulas based on the information available, such as the lengths of its diagonals or the side length with an included angle.

Below are two methods for calculating the area of a rhombus, with detailed explanations and examples for each method.

Formulas for the Area of a Rhombus

Using Diagonals:

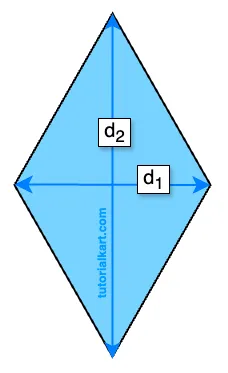
If the lengths of the diagonals \( d_1 \) and \( d_2 \) are known,

The area \( A \) can be calculated with the formula:

\( A = \dfrac{1}{2} \times d_1 \times d_2 \)

Using Side Length and Angle:

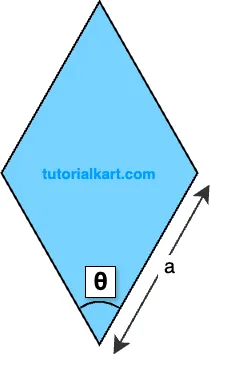
If the side length \( a \) and an interior angle \( \theta \) are known,

The area \( A \) can be calculated as:

\( A = a^2 \sin(\theta) \)

In these formulas:

• \( d_1 \) and \( d_2 \) are the lengths of the diagonals of the rhombus
• \( a \) is the length of a side of the rhombus
• \( \theta \) is the measure of one of the interior angles

---

Detailed Explanation of Each Formula

---

1. Formula for Area of a Rhombus Using Diagonals

The formula \( A = \dfrac{1}{2} \times d_1 \times d_2 \) calculates the area of a rhombus by multiplying half the product of its diagonals.

This is because the diagonals of a rhombus bisect each other at right angles, effectively dividing the rhombus into four congruent right triangles.

This formula is useful when both diagonal lengths are provided.

Example 1: Calculating Area with Given Diagonals

Problem: Find the area of a rhombus with diagonals \( d_1 = 10 \, \text{cm} \) and \( d_2 = 8 \, \text{cm} \).

Solution:

1. Write down the formula: \( A = \dfrac{1}{2} \times d_1 \times d_2 \).
2. Substitute \( d_1 = 10 \) and \( d_2 = 8 \): \( A = \dfrac{1}{2} \times 10 \times 8 \).
3. Multiply the values: \( A = \dfrac{1}{2} \times 80 = 40 \, \text{cm}^2 \).

The area of the rhombus is \( 40 \, \text{cm}^2 \).

---

2. Formula for Area of a Rhombus Using Side Length and Angle

The formula \( A = a^2 \sin(\theta) \) calculates the area of a rhombus by squaring the side length and multiplying it by the sine of one of the interior angles.

This approach is effective when the side length and one interior angle are known.

Example 2: Calculating Area with Side Length and Angle

Problem: A rhombus has a side length of \( a = 6 \, \text{cm} \) and an interior angle of \( \theta = 60^\circ \). Find the area.

Solution:

1. Write down the formula: \( A = a^2 \sin(\theta) \).
2. Substitute \( a = 6 \) and \( \theta = 60^\circ \): \( A = 6^2 \times \sin(60^\circ) \).
3. Calculate \( a^2 \): \( A = 36 \times \sin(60^\circ) \).
4. Use \( \sin(60^\circ) = \dfrac{\sqrt{3}}{2} \): \( A = 36 \times \dfrac{\sqrt{3}}{2} = 18\sqrt{3} \approx 31.18 \, \text{cm}^2 \).

The area of the rhombus is approximately \( 31.18 \, \text{cm}^2 \).

These examples demonstrate how to calculate the area of a rhombus using either the lengths of the diagonals or the side length with an interior angle, depending on the information provided.