Formula for Area of a Square – 2 Formulas with Detailed Explanation and Steps

Area of a Square Formula

The area of a square represents the space enclosed within its four equal sides.

Since all sides of a square are equal, calculating the area can be done using either the side length or the diagonal.

Below are two formulas for calculating the area of a square, with detailed explanations and examples for each method.

Formulas for the Area of a Square

Using Side Length:

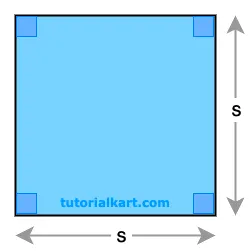
If the length of one side \( s \) of the square is known, the area \( A \) can be calculated with the formula:

\( A = s^2 \)

Using Diagonal:

If the length of the diagonal \( d \) of the square is known, the area \( A \) can be calculated as:

\( A = \dfrac{d^2}{2} \)

In these formulas:

• \( s \) is the length of a side of the square
• \( d \) is the length of the diagonal of the square

---

Detailed Explanation of Each Formula

---

1. Formula for Area of a Square using Side Length

The formula \( A = s^2 \) calculates the area of a square by squaring the length of one of its sides.

This method is straightforward, as it only requires knowing the length of one side, which is the same for all four sides in a square.

Example 1: Calculating Area with a Given Side Length

Problem: Find the area of a square with a side length of \( s = 6 \, \text{cm} \).

Solution:

1. Write down the formula: \( A = s^2 \).
2. Substitute \( s = 6 \): \( A = 6^2 \).
3. Calculate the square of the side: \( A = 36 \, \text{cm}^2 \).

The area of the square is \( 36 \, \text{cm}^2 \).

---

2. Formula for Area of a Square using Diagonal

The formula \( A = \dfrac{d^2}{2} \) calculates the area of a square using the length of its diagonal. This formula is derived from the relationship between the side and diagonal of a square.

Since the diagonal divides the square into two right-angled triangles, the diagonal length \( d \) is related to the side length \( s \) by

\( d = s\sqrt{2} \)

Using this relationship in the first formula gives the following formula.

\( A = \dfrac{d^2}{2} \).

Example 2: Calculating Area with a Given Diagonal

Problem: A square has a diagonal of \( d = 8 \, \text{cm} \). Find the area.

Solution:

1. Write down the formula: \( A = \dfrac{d^2}{2} \).
2. Substitute \( d = 8 \): \( A = \dfrac{8^2}{2} \).
3. Calculate the square of the diagonal: \( A = \dfrac{64}{2} \).
4. Simplify: \( A = 32 \, \text{cm}^2 \).

The area of the square is \( 32 \, \text{cm}^2 \).

These examples demonstrate how to calculate the area of a square using either the side length or the diagonal, making it adaptable to different types of measurements.