Area of a Trapezoid Formula
The area of a trapezoid is the space enclosed within its four sides, where two opposite sides are parallel but of different lengths. Calculating the area of a trapezoid requires knowing the lengths of the two parallel sides (often referred to as the bases) and the height (the perpendicular distance between the bases).
In this guide, we give the formula for calculating the area of a trapezoid, with a detailed explanation and example.
Formula for the Area of a Trapezoid
Using Bases and Height:
If the lengths of the two parallel sides (bases) \( a \) and \( b \), and the height \( h \) are known,
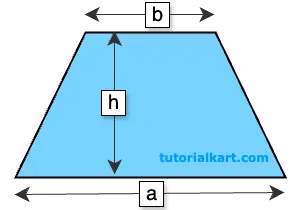
The area \( A \) can be calculated with the formula:
\( A = \dfrac{1}{2} \times (a + b) \times h \)
In this formula:
- \( a \) and \( b \) are the lengths of the two parallel sides (bases) of the trapezoid
- \( h \) is the height, or the perpendicular distance between the bases
Detailed Explanation of the Formula
Understanding the Formula
The formula \( A = \dfrac{1}{2} \times (a + b) \times h \) calculates the area of a trapezoid by averaging the lengths of the two bases and then multiplying by the height. This approach works because the height extends perpendicularly between the bases, creating a region that is effectively the “average width” of the trapezoid times the height.
Example 1: Calculating Area with Given Bases and Height
Problem: Find the area of a trapezoid with base lengths \( a = 8 \, \text{cm} \) and \( b = 5 \, \text{cm} \), and a height \( h = 4 \, \text{cm} \).
Solution:
- Write down the formula: \( A = \dfrac{1}{2} \times (a + b) \times h \).
- Substitute \( a = 8 \), \( b = 5 \), and \( h = 4 \): \( A = \dfrac{1}{2} \times (8 + 5) \times 4 \).
- Add the bases: \( A = \dfrac{1}{2} \times 13 \times 4 \).
- Multiply: \( A = \dfrac{1}{2} \times 52 = 26 \, \text{cm}^2 \).
The area of the trapezoid is \( 26 \, \text{cm}^2 \).
Example 2: Finding Height from Area and Base Lengths
Problem: A trapezoid has an area of \( A = 36 \, \text{cm}^2 \), with base lengths \( a = 10 \, \text{cm} \) and \( b = 8 \, \text{cm} \). Find the height.
Solution:
- Start with the area formula: \( A = \dfrac{1}{2} \times (a + b) \times h \).
- Substitute \( A = 36 \), \( a = 10 \), and \( b = 8 \): \( 36 = \dfrac{1}{2} \times (10 + 8) \times h \).
- Simplify inside the parentheses: \( 36 = \dfrac{1}{2} \times 18 \times h \).
- Multiply both sides by 2: \( 72 = 18h \).
- Divide by 18 to solve for \( h \): \( h = 4 \, \text{cm} \).
The height of the trapezoid is \( 4 \, \text{cm} \).
These examples show how to calculate the area of a trapezoid or find an unknown measurement based on the area formula \( A = \dfrac{1}{2} \times (a + b) \times h \).
