Area of a Triangle Formula
The area of a triangle can be calculated using several different formulas, depending on the type of information provided—such as side lengths, angles, or the coordinates of vertices.
Here is a summary of the primary formulas for finding the area of a triangle:
Using Base and Height:
\( A = \dfrac{1}{2} \times \text{base} \times \text{height} \)
Using Heron’s Formula (when all three sides are known):
\( A = \sqrt{s(s – a)(s – b)(s – c)} \), where \( s = \dfrac{a + b + c}{2} \)
Using Trigonometry (when two sides and the included angle are known):
\( A = \dfrac{1}{2} \times a \times b \times \sin(C) \)
Using Coordinates of Vertices:
\( A = \dfrac{1}{2} \left| x_1(y_2 – y_3) + x_2(y_3 – y_1) + x_3(y_1 – y_2) \right| \)
Detailed Explanation of Each Formula
1 Area of a Triangle Formula using Base and Height
This is the simplest way to calculate the area of a triangle if you know the length of its base and the perpendicular height from the base to the opposite vertex.
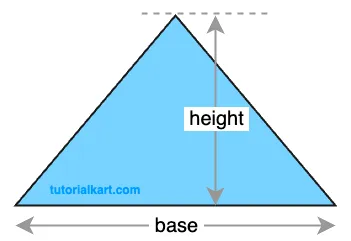
The formula for the area is
\( A = \dfrac{1}{2} \times \text{base} \times \text{height} \).
Example Problem: A triangle has a base \( AB = 6 \, \text{cm} \) and a perpendicular height from vertex \( C \) to \( AB \) as \( h = 4 \, \text{cm} \). Calculate the area of the triangle.
Solution:
- Write down the formula: \( A = \dfrac{1}{2} \times \text{base} \times \text{height} \).
- Substitute the given values: \( A = \dfrac{1}{2} \times 6 \times 4 \).
- Simplify the expression: \( A = 12 \, \text{cm}^2 \).
Thus, the area of the triangle is \( 12 \, \text{cm}^2 \).
2 Area of a Triangle Formula using Heron’s Formula
Heron’s Formula is useful when the lengths of all three sides are known.
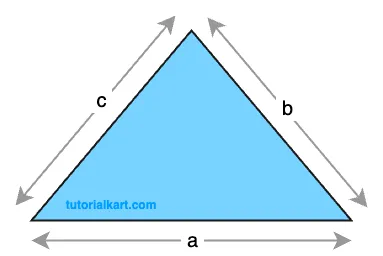
First, calculate the semi-perimeter, \( s \), which is half the sum of the sides. Then, use Heron’s formula to find the area:
\( A = \sqrt{s(s – a)(s – b)(s – c)} \), where \( s = \dfrac{a + b + c}{2} \).
Example Problem: A triangle has sides \( a = 5 \, \text{cm} \), \( b = 6 \, \text{cm} \), and \( c = 7 \, \text{cm} \). Find its area.
Solution:
- Calculate the semi-perimeter: \( s = \dfrac{5 + 6 + 7}{2} = 9 \, \text{cm} \).
- Substitute values into Heron’s formula: \( A = \sqrt{9(9 – 5)(9 – 6)(9 – 7)} \).
- Simplify: \( A = \sqrt{9 \times 4 \times 3 \times 2} = \sqrt{216} \).
- Calculate the square root: \( A \approx 14.7 \, \text{cm}^2 \).
Therefore, the area of the triangle is approximately \( 14.7 \, \text{cm}^2 \).
3 Area of a Triangle Formula using Trigonometry (Two Sides and Included Angle)
This method applies when two sides of a triangle and the angle between them are known.
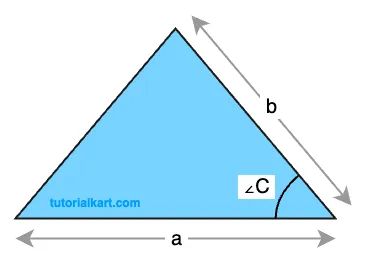
The area can be calculated by multiplying half the product of these two sides by the sine of the included angle. The formula is
\( A = \dfrac{1}{2} \times a \times b \times \sin(C) \).
Example Problem: A triangle has sides \( a = 8 \, \text{cm} \), \( b = 5 \, \text{cm} \), and the included angle \( C = 60^\circ \). Calculate the area.
Solution:
- Write down the formula: \( A = \dfrac{1}{2} \times a \times b \times \sin(C) \).
- Substitute values: \( A = \dfrac{1}{2} \times 8 \times 5 \times \sin(60^\circ) \).
- Use \( \sin(60^\circ) = \dfrac{\sqrt{3}}{2} \): \( A = \dfrac{1}{2} \times 8 \times 5 \times \dfrac{\sqrt{3}}{2} \).
- Simplify: \( A = 10\sqrt{3} \approx 17.32 \, \text{cm}^2 \).
The area of the triangle is approximately \( 17.32 \, \text{cm}^2 \).
4 Area of a Triangle Formula using Coordinates of Vertices
If the coordinates of the vertices are known, we can find the area using the determinant formula.
This formula is applicable for any triangle plotted on a coordinate plane:
\( A = \dfrac{1}{2} \left| x_1(y_2 – y_3) + x_2(y_3 – y_1) + x_3(y_1 – y_2) \right| \)
Example Problem: Given vertices \( A(1, 2) \), \( B(4, 6) \), and \( C(7, 2) \), find the area of the triangle.
Solution:
- Substitute coordinates into the formula: \( A = \dfrac{1}{2} \left| 1(6 – 2) + 4(2 – 2) + 7(2 – 6) \right| \).
- Simplify inside the absolute value: \( A = \dfrac{1}{2} \left| 1 \cdot 4 + 4 \cdot 0 + 7 \cdot (-4) \right| \).
- Continue simplifying: \( A = \dfrac{1}{2} \left| 4 – 28 \right| = \dfrac{1}{2} \times 24 = 12 \, \text{units}^2 \).
Therefore, the area of the triangle is \( 12 \, \text{units}^2 \).
Conclusion
These methods provide flexible ways to calculate the area of a triangle based on the given information, making them useful for various applications in geometry, trigonometry, and coordinate systems.
