Circumference of a Circle Formula

The circumference of a circle is the total distance around its edge.

Circumference of a Circle

You can calculate the circumference using either the radius (distance from the center to the edge) or the diameter (distance across the circle, passing through the center).

Below are the two formulas for calculating the circumference of a circle, with detailed explanations and examples for each.

Formulas for the Circumference of a Circle

Using Radius:

If the radius \( r \) of the circle is known, the circumference \( C \) can be calculated with the formula:

\( C = 2 \pi r \)

In the following diagram is a circle, with radius r marked.

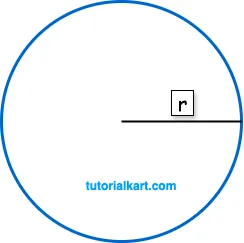
Formula for Circumference of a Circle using Radius

Using Diameter:

If the diameter \( d \) is known, the circumference \( C \) can be calculated as:

\( C = \pi d \)

In the following diagram is a circle, with diameter d marked.

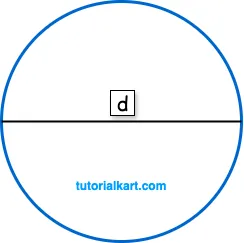
Formula for Circumference of a Circle using Diameter

In these formulas:

  • \( \pi \) (Pi) is approximately equal to 3.14159
  • \( r \) is the radius of the circle
  • \( d \) is the diameter of the circle, where \( d = 2r \)

Detailed Explanation of Each Formula

1. Formula for Circumference of a Circle using Radius

The formula \( C = 2 \pi r \) calculates the circumference of a circle by multiplying twice the radius by \( \pi \). This approach works because the diameter of the circle is twice the radius, making \( C = \pi d \) equivalent to \( C = 2 \pi r \). This formula is particularly useful when the radius is provided or easy to measure.

Example 1: Calculating Circumference with a Given Radius

Problem: Find the circumference of a circle with a radius of \( r = 7 \, \text{cm} \).

Solution:

  1. Write down the formula: \( C = 2 \pi r \).
  2. Substitute \( r = 7 \): \( C = 2 \pi \times 7 \).
  3. Multiply: \( C = 14 \pi \approx 43.98 \, \text{cm} \) (using \( \pi \approx 3.14159 \)).

The circumference of the circle is approximately \( 43.98 \, \text{cm} \).

Example 2: Finding Radius from the Circumference

Problem: A circle has a circumference of \( 31.4 \, \text{cm} \). What is its radius?

Solution:

  1. Start with the formula \( C = 2 \pi r \).
  2. Set \( C = 31.4 \) and solve for \( r \): \( 31.4 = 2 \pi r \).
  3. Divide both sides by \( 2 \pi \): \( r = \dfrac{31.4}{2 \pi} \).
  4. Approximate \( \pi \approx 3.14159 \): \( r \approx \dfrac{31.4}{6.28318} \approx 5 \, \text{cm} \).

The radius of the circle is approximately \( 5 \, \text{cm} \).

2. Formula for Circumference of a Circle using Diameter

The formula \( C = \pi d \) calculates the circumference by multiplying the diameter by \( \pi \). Since the diameter is twice the radius, this formula is equivalent to \( C = 2 \pi r \). This form is useful when the diameter is provided directly or can be easily measured.

Example 3: Calculating Circumference with a Given Diameter

Problem: A circle has a diameter of \( d = 10 \, \text{cm} \). Find the circumference.

Solution:

  1. Use the formula \( C = \pi d \).
  2. Substitute \( d = 10 \): \( C = \pi \times 10 \).
  3. Multiply by \( \pi \): \( C = 10 \pi \approx 31.42 \, \text{cm} \).

The circumference of the circle is approximately \( 31.42 \, \text{cm} \).

Example 4: Solving for Circumference in Terms of Pi with Diameter

Problem: A circle has a diameter of \( d = 12 \, \text{cm} \). Find the circumference in terms of \( \pi \).

Solution:

  1. Use the formula \( C = \pi d \).
  2. Substitute \( d = 12 \): \( C = \pi \times 12 = 12\pi \, \text{cm} \).

The circumference of the circle is \( 12\pi \, \text{cm} \) in terms of \( \pi \).

These examples illustrate how to use both forms of the circumference formula, depending on whether the radius or diameter is provided, and show how to express the answer in terms of \( \pi \) or as an approximate decimal value.