Face Diagonal of a Cube Formula
The face diagonal of a cube is the diagonal line that runs across one of the square faces of the cube.
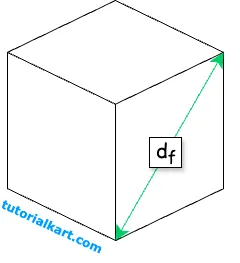
This length can be calculated if the side length of the cube is known, as it forms the hypotenuse of a right triangle on the face of the cube.
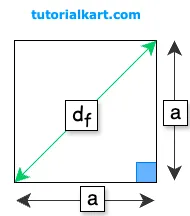
In this guide, we will go through the formula for calculating the face diagonal of a cube, along with a detailed explanation and examples.
Formula for the Face Diagonal of a Cube
Using Side Length:
If the side length \( a \) of the cube is known,
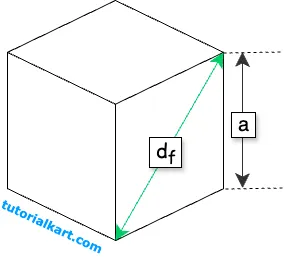
The face diagonal \( d_f \) can be calculated with the formula:
\( d_f = a\sqrt{2} \)
In this formula:
- \( a \) is the length of one side of the cube
- \( \sqrt{2} \) is the square root of 2, approximately equal to 1.414
Detailed Explanation of the Formula
The formula \( d_f = a\sqrt{2} \) calculates the face diagonal of a cube by multiplying the side length by \( \sqrt{2} \). This approach works because, on any face of the cube, the diagonal forms the hypotenuse of a right triangle, with the two sides of the square face as the legs. Using the Pythagorean theorem, we get \( d_f = \sqrt{a^2 + a^2} = a\sqrt{2} \).
Example 1: Calculating Face Diagonal with Given Side Length
Problem: Find the face diagonal of a cube with a side length of \( a = 6 \, \text{cm} \).
Solution:
- Write down the formula: \( d_f = a\sqrt{2} \).
- Substitute \( a = 6 \): \( d_f = 6 \times \sqrt{2} \).
- Approximate \( \sqrt{2} \approx 1.414 \): \( d_f \approx 6 \times 1.414 = 8.484 \, \text{cm} \).
The face diagonal of the cube is approximately \( 8.484 \, \text{cm} \).
Example 2: Finding Side Length from Face Diagonal
Problem: A cube has a face diagonal of \( d_f = 10 \, \text{cm} \). Find the side length.
Solution:
- Start with the face diagonal formula: \( d_f = a\sqrt{2} \).
- Rearrange to solve for \( a \): \( a = \dfrac{d_f}{\sqrt{2}} \).
- Substitute \( d_f = 10 \): \( a = \dfrac{10}{\sqrt{2}} \).
- Approximate \( \sqrt{2} \approx 1.414 \): \( a \approx \dfrac{10}{1.414} \approx 7.07 \, \text{cm} \).
The side length of the cube is approximately \( 7.07 \, \text{cm} \).
These examples demonstrate how to calculate the face diagonal of a cube or find an unknown side length based on the face diagonal formula \( d_f = a\sqrt{2} \).
