Finding Area of a Triangle Given Two Sides and the Included Angle

In this tutorial, we will learn how to find the area of a triangle when the lengths of two sides and the angle between them are known. This method uses a formula based on trigonometry and is simple yet powerful for calculating the area of any triangle.

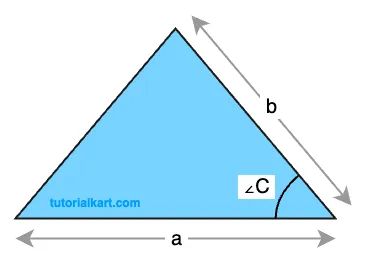
Formula

The area of a triangle with sides \(a\), \(b\), and the included angle \(C\) is given by:

\[ \text{Area} = \frac{1}{2}ab \sin(C) \]

Explanation of Terms:

  • \(a, b\): The lengths of the two known sides of the triangle.
  • \(C\): The angle (in degrees or radians) between the two sides \(a\) and \(b\).
  • \(\sin(C)\): The sine of the angle \(C\), which can be calculated using a calculator or trigonometric tables.
Area of a Triangle Formula using Trigonometry (Two Sides and Included Angle)

Examples

Example 1: Find the area of a triangle with sides 8, 10, and included angle 30°.

Given: \(a = 8\), \(b = 10\), \(C = 30^\circ\)

First, substitute the given values into the formula:

\[ \text{Area} = \frac{1}{2}ab \sin(C) \] \[ \text{Area} = \frac{1}{2} \cdot 8 \cdot 10 \cdot \sin(30^\circ) \]

Next, calculate \(\sin(30^\circ)\):

\[ \sin(30^\circ) = 0.5 \]

Now simplify:

\[ \text{Area} = \frac{1}{2} \cdot 8 \cdot 10 \cdot 0.5 = 20 \]

Answer: The area of the triangle is 20 square units.

Example 2: Find the area of a triangle with sides 7, 9, and included angle 60°.

Given: \(a = 7\), \(b = 9\), \(C = 60^\circ\)

First, substitute the given values into the formula:

\[ \text{Area} = \frac{1}{2}ab \sin(C) \] \[ \text{Area} = \frac{1}{2} \cdot 7 \cdot 9 \cdot \sin(60^\circ) \]

Next, calculate \(\sin(60^\circ)\):

\[ \sin(60^\circ) = \frac{\sqrt{3}}{2} \approx 0.866 \]

Now simplify:

\[ \text{Area} = \frac{1}{2} \cdot 7 \cdot 9 \cdot 0.866 = 27.243 \]

Answer: The area of the triangle is approximately 27.24 square units.

With this step-by-step process, you can easily find the area of any triangle given the lengths of two sides and the included angle!