Area of Right Angle Triangle
Regular methods to find area of a triangle can be used to find the area of right angle triangle when required parameters were given like three sides, or two sides and the angle between them, etc.
In this tutorial, we will discuss some specific scenarios to find the area of right angle triangle.
You can find the Area of Right Angle Triangle if you know any of the following set of parameters.
- Base and Height
- Hypotenuse and Base
- Hypotenuse and Height
- Base and Angle between Base and Hypotenuse
Area of Right Angle Triangle given Base and Height
Consider that you know base and height of a right angle triangle. Base and Height are marked on the right angle triangle in the following diagram.
\[Area\ of\ \triangle\thinspace ABC = {{Base \cdot Height} \over 2}\]
Example 1
Find area of a Right Angle Triangle whose base is 4cm and height is 6cm?
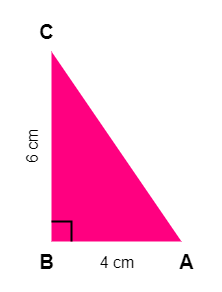
Solution:
Given Base = 4cm, Height = 6cm.
Area of Right Angle Triangle = (Base x Height)/2
= (4cm x 6cm)/2
= 12 Square cmArea of Right Angle Triangle Given Hypotenuse and Base
Now, we know how to find area of a Right Angle Triangle when base and height are given.
But, in this scenario, we are given hypotenuse instead of height.
where
- AC is hypotenuse
- AB is base
- BC is height
Using Pythagoras Theorem, we can find the height from Hypotenuse and Base. See the derivation below.
According to Pythagoras Theorem, in a Right Angle Triangle ABC, \[AC^2 = AB^2+BC^2\]
\[Height, BC = \sqrt{AC^2-AB^2}\ —–(1)\]
\[Area\ of\ \triangle\thinspace ABC = {{Base . Height} \over 2}\]
\[\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = {{AB . BC} \over 2}\ —–(2)\]
Substitude the value of \(BC\) from \((1)\) in the formula \((2)\)
\[\therefore\ Area\ of\ \triangle\thinspace ABC = {{AB . \sqrt{AC^2-AB^2}} \over 2}\]
Example 2
Find area of right angle triangle whose base is 5cm and hypotenuse is 10cm.
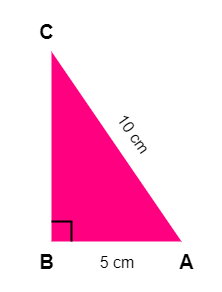
Solution:
Given
Base, AB = 5 cm
Hypotenuse, AC = 10 cm\[Area\ of\ \triangle\thinspace ABC = {{AB . \sqrt{AC^2-AB^2}} \over 2}\]
Substituting the values, \(AB=5\) and \(AC=10\) in the above equation.
\[Area\ of\ \triangle\thinspace ABC = {{5 . \sqrt{10^2-5^2}} \over 2}\]
\[Area\ of\ \triangle\thinspace ABC = {21.65\thinspace Sq.cm}\]
Area of Right Angle Triangle Given Base and Angle between Base and Hypotenuse
In this scenario, we know the length of base and the angle between base and hypotenuse.
[figure]
\[Area\ of\ \triangle\thinspace ABC = {{Base.Height} \over 2}\]
\[\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = {{AB.BC} \over 2} \ \ \ —–(1)\]
Using Trigonometry, we will apply tangent to the angle A.
\[tan \theta = {BC \over AB}\]
\[=>\ BC = AB. \ tan \theta \ \ \ —–(2)\]
Substitute the value of \((BC)\) From \((2)\) into equation \((1)\)
\[Area\ of\ \triangle\thinspace ABC = {{AB . AB .\ tan \theta} \over 2}\]
\[\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = {{AB^2\ tan \theta} \over 2}\]
