Perimeter of a Parallelogram Formula
The perimeter of a parallelogram is the total distance around the shape, calculated by summing the lengths of all four sides. Since opposite sides in a parallelogram are equal, the perimeter can be calculated if the lengths of two adjacent sides are known.
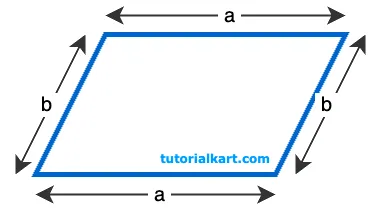
Here, we’ll go through the formula and examples for calculating the perimeter of a parallelogram.
Formula for the Perimeter of a Parallelogram
Using Adjacent Sides: If the lengths of two adjacent sides, \( a \) and \( b \), are known, the perimeter \( P \) of a parallelogram is given by:
\( P = 2(a + b) \)
In this formula:
- \( a \) is the length of one pair of opposite sides
- \( b \) is the length of the other pair of opposite sides
Detailed Explanation of the Formula
The formula \( P = 2(a + b) \) works because in a parallelogram, opposite sides are equal. So, if one pair of opposite sides has length \( a \) and the other pair has length \( b \), the total perimeter is simply twice the sum of \( a \) and \( b \). This approach makes it easy to calculate the perimeter if the lengths of any two adjacent sides are provided.
Example 1: Calculating Perimeter with Known Side Lengths
Problem: Find the perimeter of a parallelogram with side lengths \( a = 10 \, \text{cm} \) and \( b = 6 \, \text{cm} \).
Solution:
- Write down the formula: \( P = 2(a + b) \).
- Substitute the given values: \( P = 2(10 + 6) \).
- Add the side lengths inside the parentheses: \( P = 2 \times 16 \).
- Multiply by 2: \( P = 32 \, \text{cm} \).
The perimeter of the parallelogram is \( 32 \, \text{cm} \).
Example 2: Finding Perimeter When One Side Length is Doubled
Problem: A parallelogram has side lengths \( a = 12 \, \text{cm} \) and \( b = 8 \, \text{cm} \). If side \( a \) is doubled, what is the new perimeter?
Solution:
- First, calculate the new length of side \( a \): \( a = 12 \times 2 = 24 \, \text{cm} \).
- Use the perimeter formula with the updated side lengths: \( P = 2(a + b) \).
- Substitute \( a = 24 \) and \( b = 8 \): \( P = 2(24 + 8) \).
- Add the side lengths: \( P = 2 \times 32 \).
- Multiply by 2: \( P = 64 \, \text{cm} \).
The new perimeter of the parallelogram is \( 64 \, \text{cm} \).
These examples show how to calculate the perimeter of a parallelogram using the formula \( P = 2(a + b) \), whether with standard side lengths or modified values.
