Perimeter of a Square Formula
The perimeter of a square is the total distance around its four equal sides.

Calculating the perimeter can be straightforward if you know the side length or the diagonal.
Here, we’ll cover two formulas for calculating the perimeter of a square, with detailed explanations and examples for each method.
Formulas for the Perimeter of a Square
Using Side Length:
If the length of one side \( s \) of the square is known,
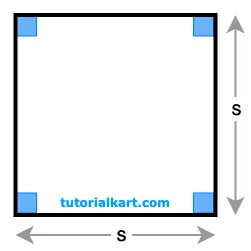
The perimeter \( P \) can be calculated with the formula:
\( P = 4s \)
Using Diagonal:
If the length of the diagonal \( d \) is known,
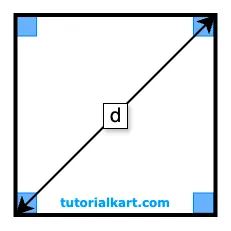
The perimeter \( P \) can be calculated as:
\( P = 2d\sqrt{2} \)
In these formulas:
- \( s \) is the length of one side of the square
- \( d \) is the length of the diagonal of the square, where \( d = s\sqrt{2} \)
Detailed Explanation of Each Formula
1 Formula for Perimeter of a Square Using Side Length
The formula \( P = 4s \) calculates the perimeter by multiplying the length of one side by 4, as all four sides in a square are equal. This formula is particularly useful when the side length is directly given or easy to measure.

Example 1: Calculating Perimeter with a Given Side Length
Problem: Find the perimeter of a square with a side length of \( s = 6 \, \text{cm} \).
Solution:
- Write down the formula: \( P = 4s \).
- Substitute \( s = 6 \): \( P = 4 \times 6 \).
- Multiply: \( P = 24 \, \text{cm} \).
The perimeter of the square is \( 24 \, \text{cm} \).
2 Formula for Perimeter of a Square Using Diagonal
The formula \( P = 2d\sqrt{2} \) calculates the perimeter by using the length of the diagonal. This method works because the diagonal of a square forms a right triangle with two adjacent sides, giving a relationship between the diagonal and side length, \( d = s\sqrt{2} \). Rearranging this relationship allows us to express the perimeter in terms of the diagonal.

Example 2: Calculating Perimeter with a Given Diagonal
Problem: A square has a diagonal of \( d = 10 \, \text{cm} \). Find the perimeter.
Solution:
- Write down the formula: \( P = 2d\sqrt{2} \).
- Substitute \( d = 10 \): \( P = 2 \times 10 \times \sqrt{2} \).
- Calculate: \( P = 20\sqrt{2} \approx 28.28 \, \text{cm} \).
The perimeter of the square is approximately \( 28.28 \, \text{cm} \).
These examples demonstrate how to calculate the perimeter of a square using either the side length or the diagonal, depending on the available measurements.
