Perimeter of a Trapezoid Formula
The perimeter of a trapezoid is the total distance around its four sides. In a trapezoid, two opposite sides are parallel but of different lengths, while the other two sides are non-parallel.

To find the perimeter, you need the lengths of all four sides. Below is the formula for calculating the perimeter of a trapezoid, with a detailed explanation and examples.
Formula for the Perimeter of a Trapezoid
Using All Four Sides:
If the lengths of the four sides \( a \), \( b \), \( c \), and \( d \) are known,
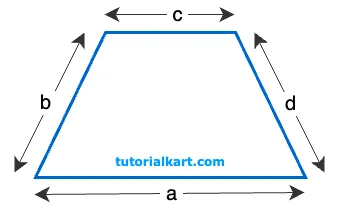
The perimeter \( P \) can be calculated with the formula:
\( P = a + b + c + d \)
In this formula:
- \( a \) and \( b \) are the lengths of the two parallel sides (bases) of the trapezoid
- \( c \) and \( d \) are the lengths of the non-parallel sides (legs) of the trapezoid
Detailed Explanation of the Formula
Understanding the Formula
The formula \( P = a + b + c + d \) calculates the perimeter of a trapezoid by simply adding the lengths of all four sides. This method is straightforward and requires knowing the lengths of both parallel and non-parallel sides of the trapezoid.
Example 1: Calculating Perimeter with Given Side Lengths
Problem: Find the perimeter of a trapezoid with side lengths \( a = 12 \, \text{cm} \), \( b = 8 \, \text{cm} \), \( c = 5 \, \text{cm} \), and \( d = 7 \, \text{cm} \).
Solution:
- Write down the formula: \( P = a + b + c + d \).
- Substitute the given values: \( P = 12 + 8 + 5 + 7 \).
- Add the side lengths: \( P = 32 \, \text{cm} \).
The perimeter of the trapezoid is \( 32 \, \text{cm} \).
Example 2: Finding a Missing Side Length from Perimeter
Problem: A trapezoid has a perimeter of \( P = 40 \, \text{cm} \), with side lengths \( a = 15 \, \text{cm} \), \( b = 10 \, \text{cm} \), and \( c = 8 \, \text{cm} \). Find the length of the fourth side \( d \).
Solution:
- Start with the perimeter formula: \( P = a + b + c + d \).
- Substitute \( P = 40 \), \( a = 15 \), \( b = 10 \), and \( c = 8 \): \( 40 = 15 + 10 + 8 + d \).
- Simplify: \( 40 = 33 + d \).
- Subtract 33 from both sides to solve for \( d \): \( d = 7 \, \text{cm} \).
The length of the fourth side \( d \) is \( 7 \, \text{cm} \).
These examples demonstrate how to calculate the perimeter of a trapezoid or find an unknown side length based on the perimeter formula \( P = a + b + c + d \).
