Perimeter of a Triangle Formula
The perimeter of a triangle is the total distance around the triangle, calculated by summing the lengths of all three sides.
There are various ways to find the perimeter, depending on the given information, such as the lengths of all three sides or two sides and the included angle.
Here, we’ll go through the formulas and examples for each approach.
Formulas for the Perimeter of a Triangle
Using Three Side Lengths:
If the lengths of all three sides are known,
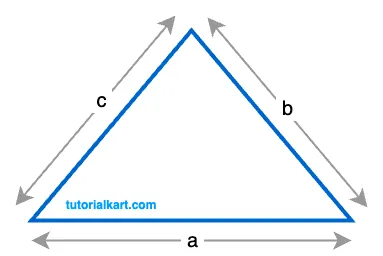
The perimeter \( P \) of a triangle is given by:
\( P = a + b + c \)
Using Two Sides and the Included Angle:
If two sides and the included angle are known,
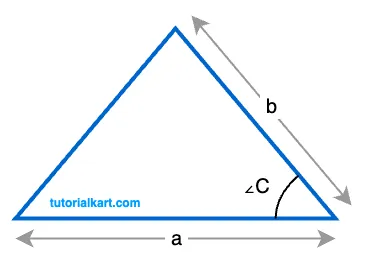
you can use the Law of Cosines to find the third side first, then sum the three sides to get the perimeter. The third side \( c \) is given by:
\( c = \sqrt{a^2 + b^2 – 2ab \cos(\theta)} \)
Then, calculate the perimeter as
\( P = a + b + c \)
In these formulas:
- \( a \), \( b \), and \( c \) are the lengths of the sides of the triangle
- \( \theta \) is the angle between sides \( a \) and \( b \)
Detailed Explanation of Each Formula
1 Perimeter of a Triangle using Three Side Lengths

If the lengths of all three sides of a triangle are known, calculating the perimeter is straightforward.
The formula
\( P = a + b + c \)
simply adds the lengths of the sides. This method is most commonly used when all sides are directly measured or given.
Example: Calculating Perimeter with Known Sides
Problem: Find the perimeter of a triangle with side lengths \( a = 5 \, \text{cm} \), \( b = 7 \, \text{cm} \), and \( c = 9 \, \text{cm} \).
Solution:
- Write down the formula:
\( P = a + b + c \). - Substitute the given values:
\( P = 5 + 7 + 9 \). - Add the side lengths:
\( P = 21 \, \text{cm} \).
The perimeter of the triangle is \( 21 \, \text{cm} \).
2 Perimeter of a Triangle using Two Sides and the Included Angle

If only two sides and the included angle are known, first calculate the third side using the Law of Cosines, then add the three sides to find the perimeter. This formula is useful for situations where all sides aren’t provided directly but can be derived.
Example: Calculating Perimeter with Two Sides and an Angle
Problem: A triangle has two sides \( a = 8 \, \text{cm} \) and \( b = 6 \, \text{cm} \) with an included angle \( \theta = 60^\circ \). Find the perimeter of the triangle.
Solution:
- Use the Law of Cosines to find the third side \( c \): \( c = \sqrt{a^2 + b^2 – 2ab \cos(\theta)} \).
- Substitute \( a = 8 \), \( b = 6 \), and \( \theta = 60^\circ \): \( c = \sqrt{8^2 + 6^2 – 2 \cdot 8 \cdot 6 \cdot \cos(60^\circ)} \).
- Calculate \( \cos(60^\circ) = 0.5 \): \( c = \sqrt{64 + 36 – 48} = \sqrt{52} \approx 7.21 \, \text{cm} \).
- Add the three sides to find the perimeter: \( P = a + b + c = 8 + 6 + 7.21 = 21.21 \, \text{cm} \).
The perimeter of the triangle is approximately \( 21.21 \, \text{cm} \).
These examples demonstrate how to calculate the perimeter of a triangle based on different sets of information, whether all three side lengths are known or only two sides and the included angle.
