Sector Area Formula
The area of a sector of a circle is the region enclosed by two radii and the corresponding arc. The area of a sector depends on the radius of the circle and the central angle of the sector.
Here, we’ll cover two formulas for calculating the area of a sector, depending on whether the central angle is given in degrees or radians, with detailed explanations and examples for each method.
Formulas for the Area of a Sector
Using Degrees:
If the radius \( r \) and the central angle \( \theta \) (in degrees) of the sector are known,
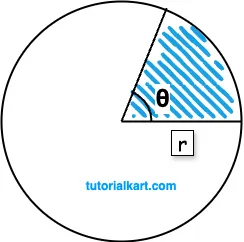
The area \( A \) can be calculated with the formula:
\( A = \dfrac{\theta}{360} \times \pi r^2 \)
Using Radians:
If the radius \( r \) and the central angle \( \theta \) (in radians) of the sector are known,
The area \( A \) can be calculated as:
\( A = \dfrac{1}{2} r^2 \theta \)
In these formulas:
- \( r \) is the radius of the circle
- \( \theta \) is the central angle of the sector in degrees or radians
- \( \pi \) (Pi) is approximately equal to 3.14159
Detailed Explanation of Each Formula
1 Formula for Sector Area Using Degrees
The formula \( A = \dfrac{\theta}{360} \times \pi r^2 \) calculates the area of a sector by finding the fraction of the circle represented by the angle \( \theta \) (in degrees) and then multiplying this fraction by the area of the entire circle \( \pi r^2 \). This formula is useful when the angle is given in degrees.

Example 1: Calculating Sector Area with a Central Angle in Degrees
Problem: Find the area of a sector with a radius of \( r = 5 \, \text{cm} \) and a central angle of \( \theta = 90^\circ \).
Solution:
- Write down the formula: \( A = \dfrac{\theta}{360} \times \pi r^2 \).
- Substitute \( r = 5 \) and \( \theta = 90 \): \( A = \dfrac{90}{360} \times \pi \times 5^2 \).
- Calculate the fraction: \( A = \dfrac{1}{4} \times \pi \times 25 \).
- Simplify: \( A = \dfrac{25\pi}{4} \approx 19.63 \, \text{cm}^2 \) (using \( \pi \approx 3.14159 \)).
The area of the sector is approximately \( 19.63 \, \text{cm}^2 \).
2 Formula for Sector Area Using Radians
The formula \( A = \dfrac{1}{2} r^2 \theta \) calculates the area of a sector by using the central angle in radians. This method is convenient when the angle \( \theta \) is provided in radians, as it allows for a straightforward calculation using the radius and angle.
Example 2: Calculating Sector Area with a Central Angle in Radians
Problem: A sector has a radius of \( r = 6 \, \text{cm} \) and a central angle of \( \theta = \dfrac{\pi}{3} \) radians. Find the area.
Solution:
- Write down the formula: \( A = \dfrac{1}{2} r^2 \theta \).
- Substitute \( r = 6 \) and \( \theta = \dfrac{\pi}{3} \): \( A = \dfrac{1}{2} \times 6^2 \times \dfrac{\pi}{3} \).
- Calculate \( r^2 \): \( A = \dfrac{1}{2} \times 36 \times \dfrac{\pi}{3} \).
- Simplify: \( A = 18 \times \dfrac{\pi}{3} = 6\pi \approx 18.85 \, \text{cm}^2 \) (using \( \pi \approx 3.14159 \)).
The area of the sector is approximately \( 18.85 \, \text{cm}^2 \).
These examples demonstrate how to calculate the area of a sector using either degrees or radians for the central angle, depending on the information provided.
