Surface Area of a Cube Formula
The surface area of a cube is the total area covered by all six faces of the cube. Since each face of a cube is a square, the surface area can be calculated using various measurements, such as the side length, the face diagonal, or the space diagonal.
Below are the formulas for calculating the surface area of a cube, with detailed explanations and examples for each method.
Formulas for the Surface Area of a Cube
Using Side Length:
If the side length \( a \) of the cube is known,
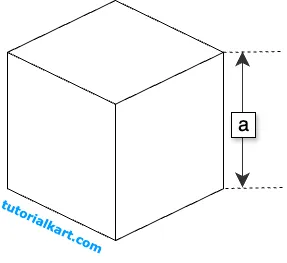
The surface area \( S \) can be calculated with the formula:
\( S = 6a^2 \)
Using Face Diagonal:
If the length of the face diagonal \( d_f \) is known,
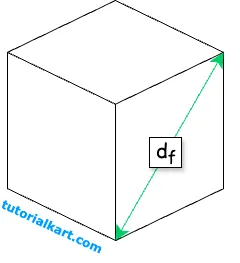
The surface area \( S \) can be calculated as:
\( S = 3d_f^2 \)
Using Space Diagonal:
If the length of the space diagonal \( d_s \) is known,
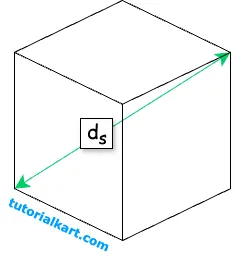
The surface area \( S \) can be calculated as:
\( S = 2d_s^2 \)
In these formulas:
- \( a \) is the length of any side of the cube
- \( d_f \) is the face diagonal, or the diagonal across one of the cube’s faces, where \( d_f = a\sqrt{2} \)
- \( d_s \) is the space diagonal, or the longest diagonal across the cube’s volume, where \( d_s = a\sqrt{3} \)
Detailed Explanation of Each Formula
1 Formula for Surface Area Using Side Length
The formula \( S = 6a^2 \) calculates the surface area by squaring the length of one side and then multiplying by 6, as each face of the cube has an area of \( a^2 \) and there are six identical faces. This method is the most straightforward when the side length is known.

Example 1: Calculating Surface Area with Given Side Length
Problem: Find the surface area of a cube with a side length of \( a = 5 \, \text{cm} \).
Solution:
- Write down the formula: \( S = 6a^2 \).
- Substitute \( a = 5 \): \( S = 6 \times 5^2 \).
- Calculate the square of the side length: \( S = 6 \times 25 = 150 \, \text{cm}^2 \).
The surface area of the cube is \( 150 \, \text{cm}^2 \).
2 Formula for Surface Area Using Face Diagonal
The formula \( S = 3d_f^2 \) calculates the surface area using the face diagonal. This formula is derived from the relationship \( d_f = a\sqrt{2} \). Rearranging this gives \( a = \dfrac{d_f}{\sqrt{2}} \), which can be substituted into the original formula \( S = 6a^2 \).

Example 2: Calculating Surface Area with Given Face Diagonal
Problem: A cube has a face diagonal of \( d_f = 6 \, \text{cm} \). Find its surface area.
Solution:
- Write down the formula: \( S = 3d_f^2 \).
- Substitute \( d_f = 6 \): \( S = 3 \times 6^2 \).
- Calculate the square of the face diagonal: \( S = 3 \times 36 = 108 \, \text{cm}^2 \).
The surface area of the cube is \( 108 \, \text{cm}^2 \).
3 Formula for Surface Area Using Space Diagonal
The formula \( S = 2d_s^2 \) calculates the surface area using the space diagonal, which is the longest diagonal in a cube. The relationship \( d_s = a\sqrt{3} \) allows us to rearrange this to find \( a \) in terms of \( d_s \) and substitute it back into the formula for surface area.

Example 3: Calculating Surface Area with Given Space Diagonal
Problem: A cube has a space diagonal of \( d_s = 7 \, \text{cm} \). Find its surface area.
Solution:
- Write down the formula: \( S = 2d_s^2 \).
- Substitute \( d_s = 7 \): \( S = 2 \times 7^2 \).
- Calculate the square of the space diagonal: \( S = 2 \times 49 = 98 \, \text{cm}^2 \).
The surface area of the cube is \( 98 \, \text{cm}^2 \).
These examples show how to calculate the surface area of a cube using different known measurements, whether it’s the side length, face diagonal, or space diagonal.
