Sorting Algorithms
Sorting algorithms are algorithms which help in arranging a list or array of elements in an order based on a feature of elements, usually quantitative.
In this tutorial, we shall look into two types of sorting algorithms based on the type of elements they work on :
- Numerical Sorting – elements in the list or array are numbers. Following are some of the numerical sorting algorithms.
– Bubble Sort
– Insertion Sort
– Selection Sort
– Heap Sort
– Merge Sort - Lexicographical Sorting – elements in the list or array are words (like in a dictionary or phone book).
Sorting Algorithms could be categorized on the basis of how they are done, resources they use, number of computations they require and so on. We shall see some of them in this tutorial.
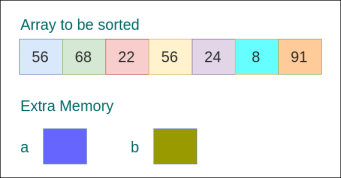
In-place Sorting
These algorithms require a fixed amount of memory irrespective of the number of elements in the array or list.
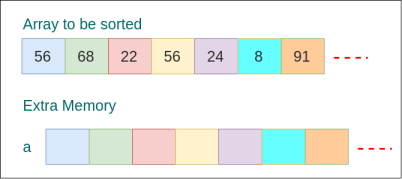
Not In-place Sorting
These algorithms require memory which is proportional to or a function of the number of elements in the array or list.
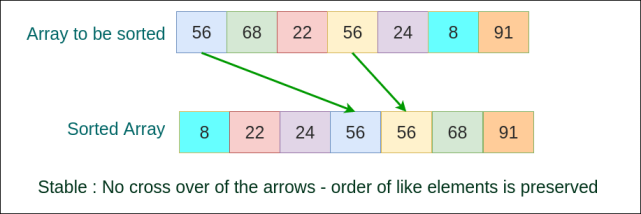
Stable Sorting
These algorithms preserve the order of similar elements in the list or array.
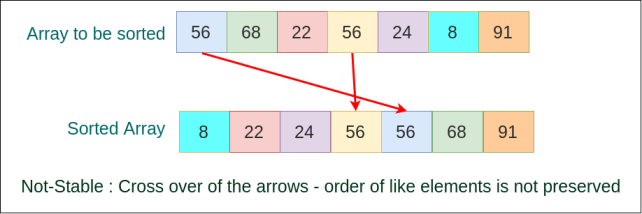
Not Stable Sorting
These algorithms may not preserve the order of similar elements in the list or array. This could possibly make the sorting process a never ending task, swapping like elements for ever. This sorting process never stops unless a break condition is provided.
Conclusion
In this tutorial, we have learnt a little about the introduction to Sorting Algorithms.